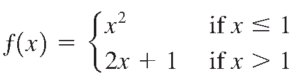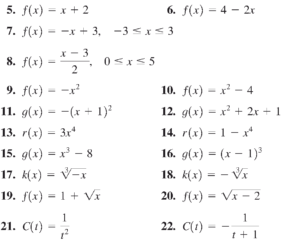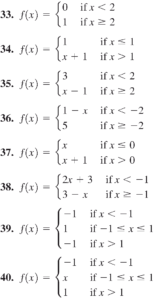۳. نمودار توابع

در درس قبل با جزئیات بیشتر به بررسی مفهوم تابع پرداختیم. در این درس با نمودار توابع و نحوه رسم آنها آشنا میشویم.

آنچه گذشت: بررسی مفهوم تابع

 

• در تعریف یک تابع خاص، متغیر $x$ در واقع موقعیتی را نشان می دهد که عضو دامنه تابع می تواند در آن قرار بگیرد.

 

• توابع چند ضابطه ای در بازه های مختلف از اعداد حقیقی ضابطه های متفاوتی دارند.

 

• نرخ تغییر: تغییر کل در مقدار تابع، وقتی متغیر مستقل از مقدار $a$ به مقدار $b$ تغییر می کند، را نرخ تغییر می نامند: $f(b)-f(a)~~~~$

 

• جدول مقادیر یک تابع جدولی با دو ستون (و یا دو سطر) است. یکی از ستون ها ورودی تابع و دیگری خروجی آن را نشان می دهد. جدول مقادیر به ما کمک می کند که تابع را به روش عددی تحلیل کنیم.

 

• دامنه تابع می تواند، به همراه تعریف تابع، از پیش مشخص شده باشد.
  هرچند، اگر دامنه تابع از پیش تعیین نشده باشد، آنگاه قرارداد معمول این است که دامنه تابع، دامنه عبارت جبری مورد نظر است (دامنه عبارت های جبری را در کتاب مقدماتی بحث کرده ایم). یعنی مجموعه همه اعداد حقیقی که برای آنها عبارت جبری مورد نظر تعریف شده است (یعنی خروجی حقیقی دارد).

 

• چهار روش برای بیان توابع: 1- توصیف تابع با استفاده از کلمات. 2- توصیف تابع با استفاده از عبارت های جبری. 3- توصیف تابع با استفاده از نمودار. 4- توصیف تابع با استفاده از شیوه عددی (جدول مقادیر).

 

 

رسم توابع با استفاده از نقطه یابی

 

نمودار یک تابع

 

برای رسم نمودار یک تابع، ما نقاط مختلف $(x,~f(x))$ را در یک صفحه مختصات رسم خواهیم کرد. به عبارت دیگر، ما نقاط $(x,~y)$ را رسم می کنیم که مولفه $x$ ورودی تابع (دامنه) و مولفه $y$ خروجی تابع (برد تابع) می باشند.

 

 

نمودار یک تابع: اگر $ f $ تابعی با دامنه$ A$ باشد، آنگاه نمودار این تابع مجموعه زوج مرتب های $~\left\lbrace (x,~f(x)) ~|~x \in A \right\rbrace ~ $  می باشد که در صفحه مختصات رسم شده است. به عبارت دیگر، نمودار تابع  $ f $ نمودار معادله $  y = f(x) $ می باشد.

 

تابعی به شکل $f(x)=mx+b$ را تابع خطی می نامیم زیرا شکل این تابع نمودار یک خط را، با شیب $m$ و عرض از مبدا $b$ نشان می دهد (پارامترهای $m$ و $b$ ثابتند). شکل زیر را ببینید.

 

 

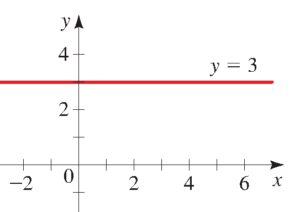
اگر $b$ یک ثابت باشد، تابعی به شکل $f(x)= b$ را یک تابع ثابت می نامیم زیرا همه خروجی های آن عدد ثابت $b$ هستند. شکل پایین را ببینید.

 

 

اگر $n$ یک عدد طبیعی باشد، توابعی به شکل $f(x)=x^{n}$ را توابع توانی و توابع به شکل $f(x)=x^{\frac{1}{n}}$ را توابع رادیکالی می نامند.

 

به رسم سه تابع $f(x)=x^{2}$، $g(x)=x^{3}$ و $h(x)=\sqrt{x}$ با استفاده از نقطه یابی دقت کنید.

 

 

 

 

 

رسم توابع با استفاده از نرم افزارها

 

یادآوری درس دوم دوره مقدمات ریاضی: رسم نمودار توابع با استفاده از نرم افزارهای محاسب و آنلاین

 

خوشبختانه هم اکنون وبسایت هایی وجود دارند که به راحتی نمودار توابع را در اختیار شما قرار می دهند. در زیر چند نمونه از این وبسایت ها را معرفی می کنیم. به جز وبسایت اول (باحساب) که به زبان فارسی است، بقیه وبسایت ها به زبان انگلیسی هستند؛ ولی معمولا کار کردن با آنها بسیار ساده است. در این میان، وولفرام آلفا که پایه نرم افزار متمتیکا است، بهترین نرم افزار محاسب آنلاین است، زیرا امکانات بسیار متنوعی دارد.

 

• https://www.bahesab.ir/calc/diagram/
• https://www.wolframalpha.com
• https://www.desmos.com/calculator
• https://www.geogebra.org/graphing?lang=en
• https://www.mathway.com/Graph

 

 شکل کلی دو وبسایت اول را در ادامه ببینید.

 

همچنین می توانید بسیاری از نرم افزارهای محاسب را بر روی گوشی خود نصب کرده و از آنها استفاده کنید.

 

 

رسم نمودار با استفاده از نرم افزارهای محاسب آنلاین

 

 

 

 

 

 

نکاتی درباره رسم توابع

 

مثال: تابع $f(x)=x^{3}-8x^{2}$ را رسم کنید.

 

پاسخ: اگر از یکی از وبسایت های محاسب باحساب و یا وولفرام استفاده کنید، چنین نموداری را برای تابع بالا خواهید دید.

 

 

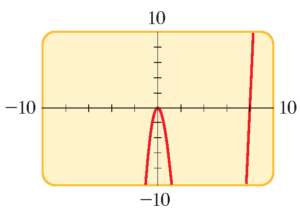
هرچند، برخی نرم افزارها و وبسایت های محاسب از شما می خواهند دامنه و برد نمودار را تعیین کنید. در این حالت بهتر است نتیجه نهایی را حتما چک کنید زیرا ممکن است شکل ناقص باشد. مثلا، اگر در تابع بالا دامنه و برد را به صورت $\left[ -10,~10 \right]$ تعیین کنیم آنگاه شکل ناکامل زیر را خواهیم دید:

 

 

نکته بسیار مهم: درک دامنه و برد توابع برای رسم آنها بسیار اهمیت دارد.

 

 

رسم توابع توانی $\textbf{f(x)=x^{n}}$

 

مثال: تابع $f(x)=x^{n}$ را برای $n=2,~4,~6$ رسم کنید.

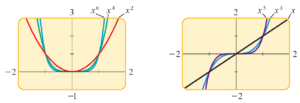
پاسخ: نمودار این سه تابع را در شکل پایین (سمت چپ) می بینید. ملاحظه می کنید که این توابع نسبت به محور عمودی متقارن هستند (درس سوم از دوره مقدمات ریاضی). در واقع توابع توانی با توان زوج رفتار بسیار مشابهی دارند.

 

 

 

مثال: تابع $f(x)=x^{n}$ را برای $n=1,~3,~5$ رسم کنید.

 

پاسخ: نمودار این سه تابع را در شکل بالا (سمت راست) می بینید. ملاحظه می کنید که این توابع نسبت به مبدا مختصات متقارن هستند (درس سوم از کتاب اول). توابع توانی با توان فرد نیز رفتار بسیار مشابهی دارند.

 

 

رسم توابع چند ضابطه ای

 

با توابع چند ضابطه ای چه کار کنیم؟!

 

توابع چندضابطه ای را باید به این صورت رسم کرد: محور اعداد حقیقی را به زیربازه های تعیین شده توسط ضابطه تابع تقسیم می کنیم. در هر زیربازه با استفاده از یک نرم افزار محاسب قسمت مورد نظر را رسم کرده و سپس همه نمودارها را با هم ادغام می کنیم.

 

توجه: وولفرام متمتیکا قابلیت تعریف توابع چندضابطه ای را دارد و برای رسم نمودار توابع چندضابطه ای بسیار مناسب است.

 

مثال: نمودار تابع زیر را رسم کنید.

 

 

پاسخ: شکل زیر را ببینید.

 

 

 

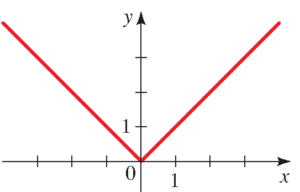
مثال: نمودار تابع قدرمطلق را رسم کنید.

 

 

پاسخ: شکل زیر را ببینید.

 

 

 

تابع جزء صحیح

 

جزء صحیح: جزء صحیح یک عدد بیشترین عدد صحیحی است که کمتر یا مساوی آن عدد است.

 

تابع جزء صحیح را با $f(x)=[x]$، $f(x)= \lfloor x \rfloor$ و یا $f(x)=\left[ [ x \right] ]$ نشان می دهند (بسته به اینکه شما کجا درس می خوانید و چه موضوعی را مطالعه می کنید!). مثال هایی از محاسبه جزء صحیح اعداد را در زیر می بینید:

 

 

شکل تابع جزء صحیح، که با استفاده از نقطه یابی بدست آمده است، را در زیر می بینید.

 

 

 

می توان جزء کسری یک عدد را نیز تعریف کرد. تابع جزء کسری را با $ \left\lbrace x \right\rbrace$ نشان می دهند.

 

 

تابع سقف

 

سقف: سقف یک عدد کوچکترین عدد صحیح بزرگتر (یا مساوی) آن عدد است. تابع سقف را به صورت $f(x)= \lceil x \rceil$ نشان می دهند.

 

تمرین: با استفاده از جدول مقادیر و نقطه یابی نشان دهید که شکل تابع سقف به صورت زیر است:

 

 

توابع پیوسته و ناپیوسته

 

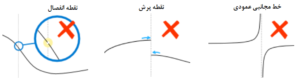
تابع پیوسته: می گوییم یک تابع پیوسته است اگر نمودار آن هیچگونه بریدگی، پرش و حفره ای نداشته باشد. تعریف توابع ناپیوسته نیز از اینجا معلوم است.

 

در شکل زیر نمونه نمونه های مختلف ناپیوستگی را ملاحظه می کنید ( منبع شکل: فرادرس ).

 

 

توابع جزء صحیح و سقف ناپیوسته هستند. از طرفی توابع $x^{n}$ و $x^{\frac{1}{n}}$ پیوسته هستند.

 

توابع جزء صحیح و سقف از انواع “توابع پله ای” هستند.

 

 

نکات مهم این درس

 

انتظار این است که در انتهای این درس شما بتوانید ویژگی های اصلی رسم نمودار توابع را به درستی توضیح داده و برخی کاربردهای آنها را بیان کنید. به ویژه انتظار می رود که بتوانید پرسش های زیر را پاسخ گویید:

 

• چطور نمودار توابع را رسم می کنیم؟
• تابع خطی چیست؟ تابع ثابت چیست؟ شکل کلی این دو تابع را بکشید.
• فرمول کلی توابع توانی و رادیکالی چیست؟
• شکل کلی تابع $x^{n}$، اگر $n$ زوج باشد، چگونه است؟
• شکل کلی تابع $x^{n}$، اگر $n$ فرد باشد، چگونه است؟
• چند وبسایت و نرم افزار برای رسم توابع را نام ببرید.
• چرا درک دامنه و برد توابع در هنگام رسم آنها مهم است؟
• توابع چندضابطه ای را چطور رسم می کنیم؟
• جزء صحیح یک عدد چیست؟ شکل تابع جزء صحیح چگونه است؟
• سقف یک عدد چیست؟ شکل تابع سقف چگونه است؟
• چه نوع توابعی را پیوسته و ناپیوسته می نامیم؟
• چند نوع تابع پیوسته و ناپیوسته مثال بزنید.

 

اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.

 

فراموش نکنیم که بهترین راه برای درک و ” درونی سازی” مفاهیم ریاضی حل مساله است. به همین دلیل سعی کنید دانسته های خود را با حل سوالات زیر محک زده و تقویت کنید.

 

 

تمرین

 

• برای تابع $f(x)=x^{2}-2$ جدول زیر را تکمیل کرده و نمودار تابع را رسم کنید.

 

 

• تعیین کنید که هرکدام از نمودارهای $I,~II,~III,~IV$ (اینها اعداد یونانی از 1 تا 4 هستند) مربوط به کدام تابع اند.

 

 

 

 

• توابع زیر را با استفاده از جدول مقادیر رسم کنید.

 

 

• با استفاده از نرم افزار و یا وبسایت محاسب دلخواه خود، توابع زیر را رسم کنید.

 

$f(x)=8x-x^{2}$

$g(x)= x^{2}-x-20$

$h(x)=x^{3}-5x-4$

$k(x)=\frac{1}{3} x^{4}-x^{2}+2$

1

1

• توابع چند ضابطه ای زیر را با استفاده از نقطه یابی رسم کنید.
  ۱

         

 

 

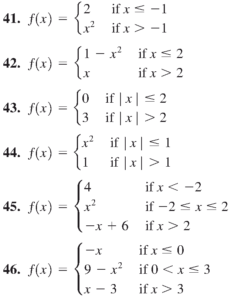
• نمودار دو تابع چندضابطه ای را ملاحظه می کنید. ضابطه این توابع را بیابید.

 

 

تمرین های جزء صحیح و سقف ( اختیاری، برای علاقمندان )

 

• اثبات کنید:

 

${\displaystyle \lfloor x\rfloor \leq x<\lfloor x\rfloor +1}$

${\displaystyle {\begin{aligned}\lfloor x\rfloor +\lfloor y\rfloor &\leq \lfloor x+y\rfloor \leq \lfloor x\rfloor +\lfloor y\rfloor +1,\\ \lceil x\rceil +\lceil y\rceil -1&\leq \lceil x+y\rceil \leq \lceil x\rceil +\lceil y\rceil .\end{aligned}}}$

${\displaystyle {\begin{aligned}x_{1}\leq x_{2}&\Rightarrow \lfloor x_{1}\rfloor \leq \lfloor x_{2}\rfloor ,\\x_{1}\leq x_{2}&\Rightarrow \lceil x_{1}\rceil \leq \lceil x_{2}\rceil .\end{aligned}}}$

$\lceil x\rceil -\lfloor x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} \end{cases}}$

${\displaystyle \lfloor x\rfloor +\lfloor -x\rfloor ={\begin{cases}0&{\text{if }}x\in \mathbb {Z} \\-1&{\text{if }}x\not \in \mathbb {Z} ,\end{cases}}}$

${\displaystyle \lceil x\rceil +\lceil -x\rceil ={\begin{cases}0&{\text{if }}x\in \mathbb {Z} \\1&{\text{if }}x\not \in \mathbb {Z} .\end{cases}}}$

مجموعه اعداد صحیح را با $\mathbb{Z}$ نشان می دهیم.

 

 

درس بعدی: تشخیص تابع

 

در جلسه بعد خواهیم آموخت که چطور می توان به دو روش نموداری و جبری توابع را تشخیص داد.

 

 

 

منابع درس

 

Algebra and Trigonometry, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 4th edition (January 13, 2015)

Precalculus: Mathematics for Calculus, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 7th edition (January 1, 2015)

 

—–

امیدوارم این درس برای شما مفید بوده باشد. لطفا اگر سوال یا نظری در مورد این درس دارید، با ما درمیان بگذارید.

 درس ها و دوره های دیگری در زمینه ریاضیات، فیزیک و نجوم هم در سایت ما (علمستان) قرار داده شده اند که میتوانید نگاهی به آنها بیندازید.