۱۲- حل معادلات و نامعادلات شامل قدرمطلق
در درس قبل با روش حل نامعادلات آشنا شدیم. در اینجا به بررسی حل معادلات و نامعادلات شامل قدرمطلق میپردازیم.
ا
آنچه گذشت: حل نامعادلات
- منظور ما از حل یک نامعادله، که شامل یک متغیر مانند $x$ می باشد، آن است که همه مقادیر این متغیر را پیدا کرده به طوری که نامعادله مورد نظر درست باشد.
۱
- برخلاف معادلات که معمولا تعداد محدودی جواب دارند، نامعادلات معمولا تعداد نامحدودی جواب دارند که تشکیل یک بازه و یا اجتماعی از بازه ها می دهند.
- برخی عملیات های جبری درست بودن نامعادلات را برهم نمی زنند. به اسلاید بعدی دقت کنید.
- یک نامعادله را نامعادله خطی می نامند اگر همه جملات آن نامعادله ثابت باشند و یا ضریب ثابتی از متغیر با توان یک باشند.
- یک نامعادله را نامعادله غیرخطی می نامند اگر شامل جملات با توان دوم و بالاتر ( و در حالت کلی جملات غیرخطی ) از متغیر باشد.
- نکاتی برای حل نامعادلات: 1- همه جملات را به یک سمت منتقل کنید. 2- تجزیه کنید. 3- بازه های مهم را بیابید. 4- یک جدول بسازید و بازه ها را تعیین علامت کنید. 5- نامعادله را حل کنید.
قوانین نامعادله ها
- با اضافه و یا کم کردن یک مقدار مشخص به دو طرف یک نامعادله، نامعادله هم ارز جدیدی حاصل خواهد شد.
$A \leq B ~~~~~\Leftrightarrow~~~~~A\pm C \leq B \pm C $
- با ضرب کردن یک مقدار مشخص مثبت در دو طرف یک نامعادله، نامعادله هم ارز جدیدی حاصل خواهد شد.
$if~~C>0~~~\Rightarrow~~~ A \leq B ~~~~~\Leftrightarrow~~~~~CA \leq CB $
- با ضرب کردن یک مقدار مشخص منفی در دو طرف یک نامعادله، نامعادله هم ارز جدیدی حاصل خواهد شد ولی جهت نامعادله برعکس می شود.
$ if~~C<0~~~\Rightarrow~~~ A \leq B ~~~~~\Leftrightarrow~~~~~CA \geq CB $
- اگر دو طرف یک نامعادله مثبت باشند، آنگاه با معکوس کردن عددها جهت نامعادله عوض می شود.
$ if~~A>0~~~and~~~B>0~~~\Rightarrow~~~ A \leq B ~~~~~\Leftrightarrow~~~~~\frac{1}{A} \geq \frac{1}{B} $
- نامعادله ها را می توان جمع کرد.
$ if~~A\leq B~~~and~~~C \leq D~~~\Rightarrow~~~ A + C \leq B+D $
- نامعادله ها خاصیت انتقالی دارند.
$if~~A\leq B~~~and~~~B \leq C~~~\Rightarrow~~~ A \leq C $
حل معادلات شامل قدرمطلق
یادآوری از دوره مقدمات ریاضی: قدرمطلق یک عدد؛ فاصله دو عدد
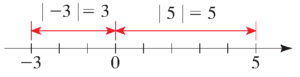
- قدر مطلق عدد $a$ به معنی فاصله عدد $a$ تا عدد صفر است:
- ویژگی های قدرمطلق:
- اگر $a$ و $b$ دو نقطه بر روی محور حقیقی باشند، فاصله (distance) بین این دو نقطه برابر است با
$d(a,b)=|a-b|$
معادلات شامل قدرمطلق
ما از ویژگی زیر برای حل معادلات شامل قدرمطلق استفاده می کنیم:
$ |x|=C~~~~~\Leftrightarrow~~~~~x=\pm C$
بنا به ویژگی بالا، برای حل معادلات شامل قدرمطلق باید دو معادله را حل کنیم. مثلا، معادله $|x|=5$ هم ارز با دو معادله $ x =5$ و $ x =-5$ می باشد. این نکته را در ذهن داشته باشیم.
مثال 1:
معادله $|2x-5|=3$ را حل کنید.
پاسخ: از معادله $|2x-5|=3$ دو معادله نتیجه می گیریم: $ 2x-5 =\pm 3~~$. حال باید این دو معادله را حل کنیم:
$ |2x-5|=3~~~~\Rightarrow~~~~2x-5=3~~~~\Rightarrow~~~~2x=8~~~~\Rightarrow~~~~x=4$
$ |2x-5|=3~~~~\Rightarrow~~~~2x-5=-3~~~~\Rightarrow~~~~2x=2~~~~\Rightarrow~~~~x=1$
درستی جواب ها را چک کنید.
مثال 2:
معادله $3| x-7|+5=14$ را حل کنید.
پاسخ: از معادله $3| x-7|+5=14$ نتیجه می گیریم:
$3| x-7|+5=14~~~~\Rightarrow~~~~3| x-7|=9~~~~\Rightarrow~~~~ | x-7|=3~~~~\Rightarrow~~~~ x-7 =\pm 3$
حال باید این دو معادله را حل کنیم:
$ x-7=3~~~~\Rightarrow~~~~ x=10~~~~~~and ~~~~~~~~x-7=-3~~~~\Rightarrow~~~~ x=4$
درستی جواب ها را چک کنید.
حل نامعادلات شامل قدرمطلق
نامعادلات شامل قدرمطلق
برای حل نامعادلات شامل قدرمطلق از ویژگی های زیر استفاده می کنیم. این ویژگی ها حتی وقتی به جای متغیر $x$ هر عبارت جبری دیگری قرار گرفته باشد، برقرار هستند.
این ویژگی ها را می توان با استفاده از تعریف قدرمطلق اثبات کرد.
مثلا، برای اثبات ویژگی اول، دقت کنید که خاصیت $|x|<c$ می گوید که فاصله عدد $x$ تا مبدا کمتر از عدد $c$ می باشد. بنا به شکل زیر، چنین گزاره ای درست است اگر و فقط اگر مقدار متغیر $x$ بین $-c$ و $c$ باشد.
تمرین: به همین صورت معنی سه ویژگی بعدی را به فارسی توضیح داده و آنها را اثبات کنید.
مثال از حل نامعادلات شامل قدرمطلق
مثال 1:
نامعادله $|x-5|<2$ را حل کنید.
پاسخ:
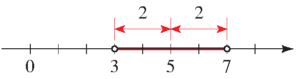
$|x-5|<2~~~~\Rightarrow~~~~-2< x-5 <2 ~~~~\Rightarrow~~~~ 3<x<7$
برای پیدا کردن نامساوی آخر، به همه جملات 5 را اضافه کرده ایم. نمودار جواب را در زیر می بینید ( به معنی هندسی جواب دقت کنید. ). درستی جواب را چک کنید.
مثال 2:
نامعادله $|3x+2|\geq 4$ را حل کنید.
پاسخ:
$|3x+2|\geq 4~~~~\Rightarrow~~~~ 3x+2 \geq 4 ~~~~\Rightarrow~~~~ 3x \geq 2 \Rightarrow~~~~ x \geq \frac{2}{3}~~~$
$|3x+2|\geq 4~~~~\Rightarrow~~~~ 3x+2 \leq -4 ~~~~\Rightarrow~~~~ 3x \leq -6 \Rightarrow~~~~ x \leq -2$
۱
پس بازه جواب ها و نمودار جواب به صورت زیرمی باشد.
نکات مهم این درس
انتظار این است که در انتهای این درس شما بتوانید ویژگی های اصلی حل معادلات و نامعادلات شامل قدرمطلق را به درستی توضیح داده و برخی کاربردهای آنها را بیان کنید. به ویژه انتظار می رود که بتوانید پرسش های زیر را پاسخ گویید:
- تعریف قدرمطلق یک عدد را بنویسید. قدرمطلق چه ویژگی هندسی را بیان می کند؟
- معنی ویژگی $~|x|=C~~\Leftrightarrow~~ x=\pm C~$ را بیان کنید.
- چهار ویژگی اساسی برای حل نامعادلات شامل قدرمطلق را بیان کنید و معنی هندسی هر کدام را نیز بیان کنید.
اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.
فراموش نکنیم که بهترین راه برای درک و ” درونی سازی” مفاهیم ریاضی حل مساله است. به همین دلیل سعی کنید دانسته های خود را با حل سوالات زیر محک زده و تقویت کنید.
تمرین های درس حل معادلات و نامعادلات شامل قدرمطلق
- معادلات زیر را حل کنید.
- نامعادلات زیر را حل کنید.
- در شکل های زیر، مجموعه هایی از اعداد حقیقی نمایش داده شده اند. برای هر شکل، نامعادله ای شامل قدرمطلق بیابید به طوری که شکل مورد نظر جواب نامعادله قدرمطلقی باشد.
درس بعدی: حل معادلات و نامعادلات به شکل نموداری
در جلسه بعد درباره حل معادلات و نامعادلات با استفاده از نمودارها بحث خواهیم کرد.
منابع درس
Algebra and Trigonometry, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 4th edition (January 13, 2015)
Precalculus: Mathematics for Calculus, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 7th edition (January 1, 2015)
—–
امیدوارم این درس برای شما مفید بوده باشد. لطفا اگر سوال یا نظری در مورد این درس دارید، با ما درمیان بگذارید.
درس ها و دوره های دیگری در زمینه ریاضیات، فیزیک و نجوم هم در سایت ما (علمستان) قرار داده شده اند که میتوانید نگاهی به آنها بیندازید.