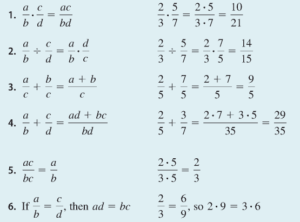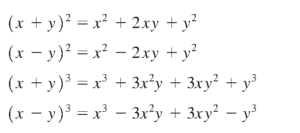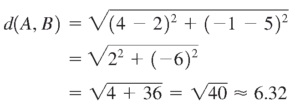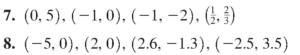۱. صفحه مختصات
اولین درس از دوره ریاضیات پایه: معادلات و نمودارها به بررسی صفحه مختصات اختصاص دارد. قبل از اینکه دوره جدید را شروع کنیم، خلاصه ای از مهمترین نکاتی که تا به حال آموخته ایم را در ادامه با هم ببینیم.
ا
آنچه گذشت: قواعد کسرها، توان، اتحادها، تجزیه
در دوره مقدمات ریاضی با اعداد حقیقی و ویژگی هایشان، قواعد کسرها، توان، اتحادها، تجزیه، و … آشنا شدیم و یاد گرفتیم چطور از آنها در مسائل ریاضی استفاده کنیم.
قواعد کسرها:
توان:
اتحادها و روابط جبری:
این دوره را با مبحث صفحه مختصات شروع میکنیم.
صفحه مختصات
صفحه مختصات ارتباط بین جبر و هندسه را برقرار می کند و از این جهت اهمیت بسیاری دارد.
در صفحه مختصات می توانیم نمودار عبارت های جبری را رسم کنیم.
از طرفی، رسم نمودار عبارت های جبری به ما قدرت شهودی برای درک رابطه بین متغیرها ( مانند افزایش و کاهش آنها، پیوستگی و … ) می دهد.
به این طریق، مسائل هندسی را می توان به طریقه روشمند جبری حل کرد و نسبت به مسائل جبری دیدگاه هندسی و شهودی پیدا کرد.
همانطور که در آینده نزدیک خواهیم دید، معرفی مفهوم “صفحه مختصات” باعث پیشرفت بسیار عظیمی در مفاهیم ریاضیاتی شده است.
نکته تاریخی
صفحه مختصات را مختصات دکارتی، و یا مختصات کارتزین ( Cartesian coordinate)، نیز می نامند. این نامگذاری به افتخار ریاضی دان و فیلسوف فرانسوی رنه دکارت (Rene Descartes) می باشد. هرچند، دیگر ریاضی دان فرانسوی، پیر فرما ( Pierre de Fermat)، نیز همزمان با دکارت این مختصات را کشف و معرفی کرده است.
انواع دیگری از مختصات (مانند مختصات قطبی، مختصات استوانه ای، مختصات کروی و …) هم وجود دارند که بعدا آنها را بررسی خواهیم کرد.

روش نوشتن مختصات یک نقطه
همانطور که هر نقطه بر روی محور را متناظر با یک عدد حقیقی دانستیم، و به این روش محور اعداد حقیقی را ساختیم، می توانیم هر نقطه در یک صفحه را متناظر با یک “زوج مرتب” دانسته و صفحه مختصات، یا مختصات دکارتی، را مطابق شکل زیر بسازیم.
منظور از زوج مرتب دو عدد به صورت $ \left( a,~b \right) $ می باشد که مولفه اول یا سمت چپ آن، یعنی $a $، نشان دهنده مختصه $ x $ و مولفه دوم یا سمت راست آن، یعنی $b $، نشان دهنده مختصه $ y $ می باشد.
برای رسم در صفحه مختصات، باید ابتدا دو محور عمود بر هم رسم کنیم. این دو محور همدیگر را در مبدا مختصات مشترک شان، یعنی نقطه 0 هر دو محور $x$ و $y$، قطع می کنند.
- معمولا یکی از محورها افقی است و جهت مثبت آن، یعنی جهت پیکان بر روی محور، به سمت راست می باشد. این محور را معمولا محور $x $ می نامند.
- محور دیگر نیز عمودی است و جهت مثبت آن معمولا به سمت بالاست. این محور را نیز معمولا محور $y$ می نامند.
ربع های مختلف صفحه مختصات:
دو محوری که در بالا گفته شد، صفحه مختصات را به چهار بخش تقسیم می کنند. این بخش ها را به ترتیب نشان داده شده در شکل بالا ربع اول تا چهارم می نامند.
مکان نقاط در صفحه مختصات:
مکان هر نقطه دلخواه مانند $P$ در صفحه مختصات را می توان با یک زوج مرتب یکتا مانند $ \left( a,~b \right) $ نشان داد. شکل زیر را ببینید. عدد اول را مختصه $x$ و یا مولفه $x$ می نامند و عدد دوم را مختصه $y$ و یا مولفه $y$ می گویند.
مختصات یک نقطه را می توان به معنی “آدرس” آن نقطه در نظر گرفت!
توجه: گرچه نمادگذاری مورد استفاده برای نشان دادن یک نقطه، یعنی $ \left( a,~b \right) $، با نمادگذاری مورد استفاده برای بازه باز، یعنی $ \left( a,~b \right) $، یکسان است، معمولا در متن مشخص است که منظور کدام است. این شباهت نه چندان خوشایند را به یاد داشته باشید!
روش پیدا کردن مختصات یک نقطه:
از نقطه مورد نظر به موازات محور $y$ خطی عمودی رسم کنید. محل تلاقی این خط با محور $x$ را مولفه $x$ آن نقطه می گویند (در شکل بالا سمت چپ با $ a $ مشخص شده است). به همین صورت، از نقطه مورد نظر به موازات محور $x$ خطی افقی رسم کنید. محل تلاقی این خط با محور $y$ را مولفه $y$ آن نقطه می گویند ( $ b $ در شکل بالا).
بنابراین مختصات نقطه مورد نظر را با $ \left( a,~b \right) $ و یا $P \left( a,~b \right) $ نشان می دهند.
مجددا به مثال های موجود در این شکل دقت کنید.
رسم یک ناحیه در صفحه مختصات
میتوان رفتار عبارت های جبری، توابع ( موضوع دوره های بعدی )، بازه ها و ناحیه ها را در صفحه مختصات دید. مثلا فرض کنید که می خواهیم سه ناحیه زیر را در صفحه مختصات رسم کنیم.
- اولی، نشان دهنده مجموعه نقاطی در صفحه مختصات است که مولفه $x$ آنها نامنفی ولی مولفه $y$ آنها دلخواه است. به توپر بودن خط مرزی $x=0$ دقت کنید.
- دومی، نشان دهنده مجموعه نقاطی در صفحه مختصات است که مولفه $x$ آنها دلخواه ولی مولفه $y$ آنها برابر 1 است.
- سومی، نشان دهنده مجموعه نقاطی در صفحه مختصات است که مولفه $x$ آنها دلخواه ولی مولفه $y$ آنها بین $ -1 $ تا 1 است. به خط چین بودن خطوط مرزی این ناحیه دقت کنید.
نتیجه را در در شکل زیر می بینید.
علامت مختصه های $x$ و $y$ در چهار ربع صفحه مختصات
به علامت مختصه های $x$ و $y$ در چهار ربع صفحه مختصات در شکل زیر (سمت چپ) دقت کنید. توجه کنید که در بالای محور $x$ها مقدار $y$ مثبت بوده و در پایین آن مقدار $y$ منفی است. همچنین، در سمت راست محور $y$ ها مقدار $x$ مثبت بوده و در سمت چپ آن مقدار $x$ منفی است.
حالا به نقاط مشخص شده در شکل سمت راست دقت کرده و مطمئن شوید که این نقاط علامت درستی دارند.
فاصله
یادآوری از دوره مقدمات ریاضی: قدرمطلق یک عدد؛ فاصله دو عدد
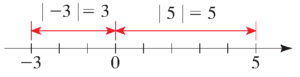
قدر مطلق عدد $a$ به معنی فاصله عدد $a$ تا عدد صفر است:
ویژگی های قدرمطلق:
اگر $a$ و $b$ دو نقطه بر روی محور حقیقی باشند، فاصله ($ distance $) بین این دو نقطه برابر است با
$d(a,b)=|a-b|$
فاصله دو نقطه در صفحه مختصات
برای پیدا کردن فاصله بین دو نقطه دلخواه در صفحه مختصات، مانند نقاط $A \left(x_{1},~y_{1} \right)$ و $B \left(x_{2},~y_{2} \right)$، باید از قضیه فیثاغورس استفاده کنیم.
- از نقطه $A$ خطی به موازات محور $x$ و از نقطه $B$ خطی به موازات محور $y$ رسم می کنیم. این دو خط بر هم عمود بوده و همدیگر را در نقطه $C$ قطع می کنند.
- از مباحث دوره مقدمات ریاضی می دانیم که فاصله بین نقاط $A$ و $C$ برابر است با $|x_{2}-x_{1}|$.
- از طرفی می دانیم که فاصله بین نقاط $B$ و $C$ برابر است با $|y_{2}-y_{1}|$. بنابراین طول اضلاع مثلث قائم الزاویه معلوم می شود.
- بنا به قضیه فیثاغورس، فاصله بین نقاط $A $ و $ B$ برابر طول وتر این مثلث قائم الزاویه است:
$d \left(A,~B \right) =\sqrt{|x_{2}-x_{1}|^{2}+|y_{2}-y_{1}|^{2}}= \sqrt{( x_{2}-x_{1} )^{2}+ (y_{2}-y_{1})^{2}} $
- فاصله بین دو نقطه $A \left(x_{1},~y_{1} \right)$ و $B \left(x_{2},~y_{2} \right)$ برابر است با:
$ d \left(A,~B \right) = \sqrt{( x_{2}-x_{1} )^{2}+ (y_{2}-y_{1})^{2}} $
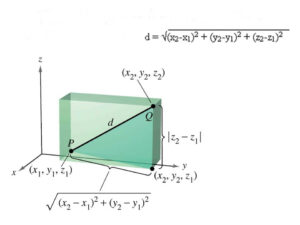
در آینده فاصله بین دو نقطه در فضای سه بعدی را نیز به دست خواهیم آورد.
مثال: یافتن فاصله بین دو نقطه
- فاصله بین دو نقطه $A $ و $B$ در شکل زیر را بیابید.
پاسخ:
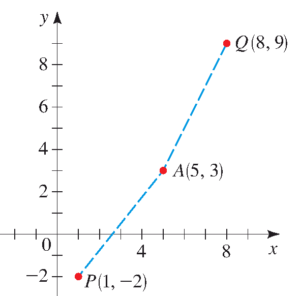
- کدام یک از نقاط $P $ و یا $Q$ در شکل زیر به نقطه $A$ نزدیکترند؟
پاسخ: فاصله هر دو نقطه $P $ و $Q$ نسبت به نقطه $A$ را به دست آورده و با هم مقایسه می کنیم:
بنابراین نقطه $P $ به نقطه $A$ نزدیکتر است.
نقطه میانی
نقطه میانی ($Midpoint$) بین دو نقطه $A$ و $B$ نقطه ای است که فاصله اش تا نقطه $A$ برابر با فاصله اش تا نقطه $B$ باشد. یعنی اگر نقطه میانی را با $M$ نشان دهیم، آنگاه
$d(A,~M)=d(M,~B)$
حال می خواهیم مختصات نقطه میانی بین دو نقطه $A$ و $B$ را بیابیم. برای انجام اینکار فرض کنید مختصات این نقطه را با $M(x,~y)$ و مختصات دو نقطه دیگر را با $A(x_{1},~y_{1})$ و $B(x_{2},~y_{2})$ نشان می دهیم.
از شکل بالا می توان به راحتی فهمید که دو مثلث قائم الزاویه $APM$ و $MQB$ هم نهشت ( یعنی هم ارز، یکسان ) هستند. چرا؟
یادآوری از هم نهشتی مثلث های قائم الزاویه:
- وتر و یک ضلع از یک مثلث با وتر و یک ضلع از مثلث دیگر مساوی باشد.
- وتر و یک زاویه از یک مثلث با وتر و یک زاویه از مثلثی دیگر مساوی باشد.
بنا به برابر بودن وتر و زاویه قائمه، دو مثلث قائم الزاویه $APM$ و $MQB$ هم نهشت هستند.
با توجه به هم نهشتی دو مثلث نشان داده شده در شکل، اضلاع متناظر این دو مثلث با هم برابر هستند؛ یعنی
$d(A,~P)=d(M,~Q)~~~~~\Rightarrow~~~~~x-x_{1}=x_{2}-x~~~~~\Rightarrow~~~~~2x=x_{2}+x_{1}$
$d(P,~M)=d(Q,~B)~~~~~\Rightarrow~~~~~y-y_{1}=y_{2}-y~~~~~\Rightarrow~~~~~2y=y_{2}+y_{1}$
بنابراین، مختصات نقطه میانی بین دو نقطه $A(x_{1},~y_{1})$ و $B(x_{2},~y_{2})$ به صورت زیر است:
$\left( \frac{x_{1}+x_{2}}{2},~ \frac{y_{1}+y_{2}}{2} \right)$
مثال ۱:
نقطه میانی بین دو نقطه $(-2,~1) $ و $(4,~5) $ را بیابید. شکل زیر را ببینید.
پاسخ:
$\left( \frac{-2+4}{2},~ \frac{1+5}{2} \right)=\left( 1,~ 3 \right)$
مثال ۲:
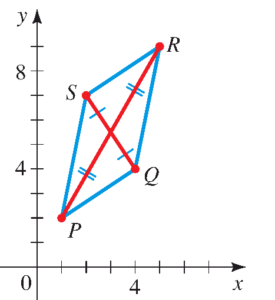
نشان دهید که چهارضلعی (quadrilateral) زیر با رئوس $P(1,~2)$، $Q(4,~4)$، $R(5,~9)$ و $S(2,~7)$ در واقع یک متوازی الاضلاع (parallelogram) می باشد.
راهنمایی: در متوازی الاضلاع، قطرها همدیگر را نصف می کنند.
پاسخ:
اگر نقطه میانی هر دو قطر بر هم منطبق باشد ( یعنی مختصات نقطه میانی دو قطر یکسان باشد. ) آنگاه دو قطر همدیگر را نصف می کنند. نقطه میانی قطر $PR$ برابر است با:
$\left( \frac{1+5}{2},~ \frac{2+9}{2} \right)=\left( 3,~ \frac{11}{2} \right)$
همچنین، نقطه میانی قطر $SQ$ برابر است با:
$\left( \frac{4+2}{2},~ \frac{4+7}{2} \right)=\left( 3,~ \frac{11}{2} \right)$
نکات مهم این درس
انتظار این است که در انتهای این درس شما بتوانید ویژگی های اصلی مختصات کارتزین، فاصله دو نقطه و نقطه میانی بین دو نقطه را به درستی توضیح داده و برخی کاربردهای آنها را بیان کنید. به ویژه انتظار می رود که بتوانید پرسش های زیر را پاسخ گویید:
- چرا معرفی صفحه مختصات اهمیت بسیاری دارد؟
- اسامی مختلف مختصات دکارتی را بیان کنید.
- منظور از زوج مرتب چیست؟ در یک زوج مرتب، کدام مولفه نشان دهنده مختصه افقی و کدام نشان دهنده مختصه عمودی است؟
- طریقه رسم محورهای مختصات و تشکیل مختصات دکارتی را بیان کنید. مبدا مختصات در کجا قرار دارد؟
- نامگذاری معمول محورهای افقی و عمودی چگونه است؟ جهت معمول هر محور را نیز بیان کنید.
- چهار ربع صفحه مختصات را با رسم شکل نشان داده و علامت مختصه های $x$ و $y$ در هر ربع را بیان کنید.
- روش پیدا کردن مختصات یک نقطه دلخواه در صفحه مختصات را بیان کنید.
- ناحیه های مختلف در صفحه مختصات را چطور می توان از لحاظ جبری بیان کرده و در صفحه مختصات نمایش داد؟ باز و بسته بودن نواحی چطور نشان داده می شود؟
- رابطه تعیین کننده فاصله بین نقاط $A \left(x_{1},~y_{1} \right)$ و $B \left(x_{2},~y_{2} \right)$ را بنویسید. چطور این رابطه را به دست می آوریم؟
- رابطه تعیین کننده نقطه میانی بین نقاط $A \left(x_{1},~y_{1} \right)$ و $B \left(x_{2},~y_{2} \right)$ را بنویسید. چطور این رابطه را به دست می آوریم؟
- شرایط همنهشتی دو مثلث قائم الزاویه کدامند؟
- یکی از ویژگی های مهم دو قطر در متوازی الاضلاع را بیان کنید.
اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.
فراموش نکنیم که بهترین راه برای درک و ” درونی سازی” مفاهیم ریاضی حل مساله است. به همین دلیل سعی کنید دانسته های خود را با حل سوالات زیر محک زده و تقویت کنید.
تمرین
- در شکل زیر مختصات همه نقاط از $A$ تا $H$ را بنویسید. مثلا $A(5,~1)$ و … .
- در شکل بالا تعیین کنید که نقاط یاد شده در کدام ربع از صفحه مختصات قرار دارند. همچنین، مجموعه نقاط موجود در ربع سوم را بنویسید.
- دستگاه مختصاتی رسم کرده و نقاط زیر را در آن نمایش دهید.
- نواحی زیر را در دستگاه مختصات نمایش دهید. برای هر ناحیه یک دستگاه مختصات رسم کنید.
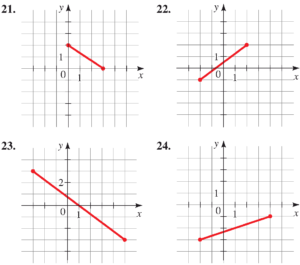
- در هر کدام از شکل های زیر،
ا الف) مختصات دو نقطه ابتدایی و انتهایی پاره خط را بنویسید.
ا ب) فاصله دو نقطه ( و یا به عبارتی طول پاره خط ) را بیابید.
ا پ) مختصات نقطه میانی پاره خط را بیابید.
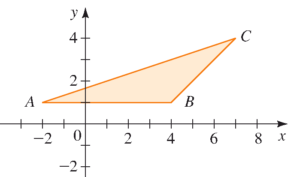
- در شکل زیر مساحت مثلث را بیابید.
راهنمایی: پاره خط $AB$ موازی محور افقی است.
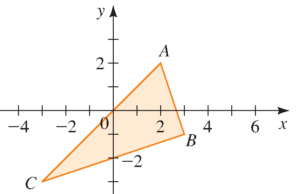
- در شکل زیر،
ا الف) با استفاده از معکوس قضیه فیثاغورس نشان دهید که مثلث مورد نظر قائم الزاویه است.
ا ب) مساحت مثلث را بیابید.
- در شکل زیر، نقطه $M$ نقطه میانی پاره خط $AB$ می باشد.
ا الف) مختصات نقطه $M$ را بیابید.
ا ب) فاصله نقطه $M$ تا هر کدام از رئوس مثلث را بیابید.
ا پ) چه نتیجه ای درباره این سه فاصله می گیرید؟
یک نکته و یک تمرین
نکته:
برای پیدا کردن قرینه یک نقطه مانند $A(x,~y)$ نسبت به محور عمودی $y$ فقط کافی است که مولفه $x$ را قرینه کنیم. یعنی اگر قرینه نقطه $A$ نسبت به محور عمودی $y$ را با $A^{\prime}$ نشان دهیم، آنگاه: $A^{\prime}(-x,~y)$
برای پیدا کردن قرینه یک نقطه مانند $A(x,~y)$ نسبت به محور افقی $x$ فقط کافی است که مولفه $y$ را قرینه کنیم. یعنی اگر قرینه نقطه $A$ نسبت به محور افقی $x$ را با $A^{\prime \prime}$ نشان دهیم، آنگاه: $A^{\prime \prime}(x,~-y)$
پرسش:
الف) در شکل بالا قرینه مثلث قرمز رنگ نسبت به محور عمود رسم شده است. مختصات رئوس مثلث قرینه، یعنی مثلث آبی رنگ، را بیابید.
ب) قرینه مثلث قرمز رنگ نسبت به محور افق را رسم کرده و مختصات رئوس آن را بیابید.
درس بعدی: رسم نمودارها با نقطه یابی و تقاطع نمودار با محورهای مختصات
یکی از اصلی ترین کاربردهای صفحه مختصات، رسم نمودار عبارت های جبری در این صفحه است. در جلسه بعد، با آسان ترین روش رسم نمودار به نام نقطه یابی آشنا خواهیم شد. خواهیم آموخت که چطور با عددگذاری می توان برداشتی کلی از رفتار عبارت های جبری داشت.
همچنین می آموزیم که چطور می توان نقطه تلاقی نمودارها با محورهای مختصات را یافت. این یکی از مهم ترین مسائلی است که در این کتاب ها با آن روبرو خواهیم شد و از چند دیدگاه مختلف به آن خواهیم نگریست.


منابع درس
Algebra and Trigonometry, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 4th edition (January 13, 2015)
Precalculus: Mathematics for Calculus, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 7th edition (January 1, 2015)
—–
امیدوارم این درس برای شما مفید بوده باشد. لطفا اگر سوال یا نظری در مورد این درس دارید، با ما درمیان بگذارید.
درس ها و دوره های دیگری در زمینه ریاضیات، فیزیک و نجوم هم در سایت ما (علمستان) قرار داده شده اند که میتوانید نگاهی به آنها بیندازید.