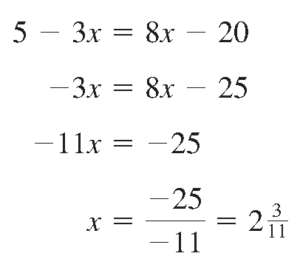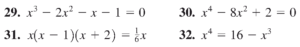۱۳- حل معادلات و نامعادلات به شکل نموداری

در درس قبل با روش حل معادلات و نامعادلات شامل قدرمطلق آشنا شدیم. در این درس به بررسی حل معادلات و نامعادلات به شکل نموداری میپردازیم.

ا

آنچه گذشت: حل معادلات و نامعادلات شامل قدرمطلق

 

• ما از ویژگی زیر برای حل معادلات شامل قدرمطلق استفاده می کنیم:

$|x|=C~~~~~\Leftrightarrow~~~~~x=\pm C$

 

• برای حل نامعادلات شامل قدرمطلق از ویژگی های زیر استفاده می کنیم. این ویژگی ها، حتی وقتی به جای متغیر$x$ هر عبارت جبری دیگری قرار گرفته باشد، برقرار هستند.
  م

 

 

حل معادلات به شکل نموداری

 

حل معادلات به روش جبری و به روش نموداری

 

تاکنون در دوره مقدمات ریاضی و دوره حاضر یاد گرفته ایم که چطور معادلات را بوسیله روش های جبری حل کنیم. در چنین روشی ما متغیر $x$ را به عنوان مجهول در نظر گرفته و بوسیله قوانین جبری آن را در یک طرف تساوی منزوی کرده و مقدار آن را پیدا می کنیم. همچنین در بخش های قبل آموختیم که چطور نامعادلات را به روش مشابهی حل کنیم.

 

بعضی اوقات ممکن است که نتوان به سادگی یک معادله و یا نامعادله را به روش های جبری حل کرد. در این حالت می توانیم از روش نموداری برای حل مساله استفاده کنیم.

 

در این روش، ما $x$ را به عنوان یک متغیر در نظر گرفته و نمودار مناسبی را برای توصیف وضعیت رسم می کنیم. آنگاه می توانیم مقادیری را که متغیر $x$ می تواند بپذیرد، تا معادله حل شود، بیابیم.

 

روش حل نموداری معادلات و نامعادلات پایه روش های عددی برای حل معادلات و نامعادلات است و به همین جهت اهمیت اساسی دارد.

 

 

 

حل معادلات با استفاده از نمودارها

 

 

برای حل یک معادله یک متغیره، مانند $3x-5=0$، با استفاده از نمودار، نخست نمودار معادله دو متغیره $y=3x-5$ را رسم می کنیم. دقت کنید که این معادله با جایگزین کردن طرف صفر معادله اصلی با متغیر $y$ بدست آمده است. جواب های معادله مورد نظر مقادیری از متغیر $x $ هستند که برای آنها متغیر $y $ صفر می شود. یعنی، همانطور که قبلا نیز گفته شده است، جواب های معادله مقادیر طول از مبدا نمودار هستند. به مثال زیر دقت کنید.

مثال: حل نموداری معادله $3x-4=1$:

 

$3x-4=1~~~~\Rightarrow~~~~3x-5=0~~~~\Rightarrow~~~~y=3x-5$

 

پس باید نمودار معادله $y=3x-5$ را رسم کنیم. اینکار را در شکل زیر انجام داده ایم و از اینجا معلوم است که جواب تقریبی $x \approx 1.7$ می باشد.

 

 

 

مثال: حل جبری معادله $3x-4=1$:

 

$3x-4=1~~~~\Rightarrow~~~~3x=5~~~~\Rightarrow~~~~x=\frac{5}{3}$

 

برتری روش جبری این است که جواب های دقیقی به ما می دهد. همچنین، فرایند حل معادلات به ما کمک می کند که ساختار جبری معادلات، و قوانین جبر، را بهتر بشناسیم.

 

از طرف دیگر، بسیاری از معادلات را نمی توان به راحتی به صورت جبری حل کرد. در این حالت، روش نموداری یک جواب تقریبی ارزشمند در اختیار ما قرار می دهد. همچنین، رسم نمودارها باعث می شود که ما دیدگاه خوبی نسبت به رفتار معادلات پیدا کنیم.

 

 

حل معادلات درجه دوم به روش نموداری

 

همه جواب های حقیقی سه معادله درجه دوم زیر را بیابید:

 

$(a)~x^{2}-4x+2=0~~~~~~~~~~(b)~x^{2}-4x+4=0~~~~~~~~~~(c)~x^{2}-4x+6=0$

 

یادآوری روش جبری: جواب هر کدام از این معادلات را می توان با استفاده از روش دلتا به راحتی پیدا کرد:

 

$ x_{1},~x_{2}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

 

با استفاده از فرمول بالا برای هر کدام از معادلات داریم:

 

$ (a)~x^{2}-4x+2=0~~~~~\Rightarrow~~~~~ x_{1},~x_{2}=2 \pm \sqrt{2}$

$ (b)~x^{2}-4x+4=0~~~~~\Rightarrow~~~~~ x_{1}=x_{2}=2 $

$ (c)~x^{2}-4x+6=0~~~~~\Rightarrow~~~~~ x_{1},~x_{2}=2 \pm i\sqrt{2}$

معادله آخر جواب حقیقی ندارد زیرا دلتای آن منفی است.

 

روش نموداری: نمودارها را با استفاده از یک وبسایت و یا نرم افزار محاسب رسم می کنیم ( و یا از نقطه یابی استفاده می کنیم ). در درس دوم از دوره حاضر با وبسایت زیر آشنا شدیم:

 https://www.bahesab.ir/calc/diagram/

نتیجه را در شکل های زیر می بینید.

• در مورد اول، ریشه ها به صورت تقریبی $x \approx 0.6$ و $x \approx 3.4$ پیدا می شوند.
• در مورد دوم، تنها یک ریشه در $x = 2$ داریم.
• در مورد سوم هیچ محل تقاطعی با محور افقی وجود ندارد؛ بنابراین مورد سوم جواب ندارد.

 

 

 

مثالی دیگر از حل معادله به روش نموداری

1

معادله $ 5-3x=8x-20$ را به روش جبری و نموداری حل کنید.

 

نتیجه روش جبری را در زیر می بینید.

 

 

در روش نموداری، می توانیم همه جملات را به یک سمت برده و در انتها معادله حاصله ($y=11x-25$) را رسم کنیم و جواب را بیابیم ($x \approx 2.27$).

 

ولی اگر بخواهیم حتی از این جزییات جبری نیز عبور کنیم می توانیم نمودارهای خطوط $y_{1}=5-3x$ و $y_{2}= 8x-20$ را رسم کرده و نقطه تقاطع آنها را بیابیم. این نقطه، مطابق شکل زیر در $x \approx 2.27$ و $y \approx -1.81$ رخ می دهد که البته فقط مولفه اول برای ما مهم است.

1

 

 

حل معادله در یک بازه خاص به روش نموداری

 

معادله $ x^{3}-6x^{2}+9x=\sqrt{x}$ را در بازه $\left[ 1,~6\right]$ به روش نموداری حل کنید.

 

همه جملات را به یک سمت برده

 

$ x^{3}-6x^{2}+9x-\sqrt{x}=0$

 

و در انتها معادله مورد نیاز برای رسم نمودار را می یابیم:

 

$y= x^{3}-6x^{2}+9x-\sqrt{x} $

 

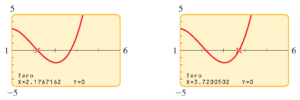
این معادله را در بازه مورد نظر رسم کرده و نقاط تقاطع نمودار با محور افقی را می یابیم. دو نقطه تقاطع در $x \approx 2.18$ و $x \approx 3.72$ وجود دارد.

 

 

1

حل نامعادلات به شکل نموداری

 

حل نامعادلات با استفاده از رسم نمودارها

 

برای حل یک نامعادله یک متغیره، مانند $3x-5 \geq 0$، با استفاده از نمودار، نخست نمودار معادله دو متغیره $y=3x-5$ را رسم می کنیم. دقت کنید که این معادله با جایگزین کردن طرف صفر نامعادله اصلی با متغیر $y$ بدست آمده است. جواب های نامعادله مورد نظر مقادیری از متغیر $x $ هستند که برای آنها متغیر $y $ بزرگتر یا مساوی صفر می شود. یعنی، جواب های معادله مقادیری از متغیر $x $ هستند که برای آنها متغیر $y $ در بالای محور افقی قرار میگیرد. برای نامعادله های دیگر نیز به روشی مشابه عمل می کنیم. به مثال های زیر دقت کنید.

 

مثال:

• حل نموداری معادله $3x-4 \geq 1$:

 

$3x-4 \geq 1~~~~\Rightarrow~~~~3x-5\geq 0~~~~\Rightarrow~~~~y=3x-5$

 

پس باید نمودار معادله $y=3x-5$ را رسم کنیم. اینکار را در شکل زیر انجام داده ایم و از اینجا معلوم است که جواب تقریبی $x \gtrsim 1.7$ می باشد. یعنی برای مقادیر $x \gtrsim 1.7$، مقدار متغیر $y$، و یا همان $3x-5$، بزرگتر از صفر است.

 

 

• حل جبری معادله $3x-4 \geq 1$:

 

$3x-4 \geq 1~~~~\Rightarrow~~~~3x \geq 5~~~~\Rightarrow~~~~x \geq \frac{5}{3}$

 

 

مثال های دیگر از حل نامعادلات به روش نموداری

 

مثال:

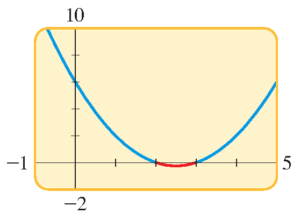
نامعادله $ x^{2}-5x+6 \leq 0$ را به روش نموداری حل کنید.

 

این نامعادله را قبلا به روش جبری حل کرده ایم (درس یازدهم این دوره). برای حل معادله به روش نموداری، نمودار معادله $y= x^{2}-5x+6 $ را رسم می کنیم. شکل زیر را ببینید. هدف ما این است که مقادیری از متغیر $x $ را بیابیم که به ازای آنها کمیت $ x^{2}-5x+6 $، و یا همان $y$، پایین محور افقی قرار گیرد. بنابراین، از شکل مقابل درمی یابیم که جواب نامعادله بازه $\left[ 2,~ 3 \right]$ می باشد.

1

مثال:

نامعادله $ 3.7x^{2}+1.3x-1.9 \leq 2.0-1.4x$ را به روش نموداری حل کنید.

 

می توانیم نمودارهای معادلات

$y_{1}=3.7x^{2}+1.3x-1.9~~~~~~~~~~~~~~~~~~~y_{2}= 2.0-1.4x$

را رسم کرده و نقاط تقاطع آنها را بیابیم. این نقاط، مطابق شکل در $x \approx -1.45$ و $x \approx 0.72$ رخ می دهند. جواب مد نظر ما، مقادیری از $x $ است که در آن $y_{1} \leq y_{1}$؛ یعنی نمودار $y_{1} $ زیر نمودار $y_{2} $ قرار می گیرد. پس بازه جواب به صورت تقریبی $-1.45 \lesssim x \lesssim 0.72$ می باشد.

 

 

 

مثال:

نامعادله $x^{3} -5x^{2} \geq -8$ را به روش نموداری حل کنید.

 

برای حل معادله به روش نموداری، نمودار معادله $y= x^{3} -5x^{2}+8 $ را رسم می کنیم. شکل مقابل را ببینید. هدف ما این است که مقادیری از متغیر $x $ را بیابیم که به ازای آنها کمیت $ x^{3} -5x^{2}+8 $، و یا همان $y$، بالای محور افقی قرار گیرد. بنابراین، از شکل مقابل درمی یابیم که جواب نامعادله به صورت تقریبی بازه

 

$\left[ -1.1,~ 1.5 \right] \cup \left[4.6,~ \infty \right)$

می باشد.

 

 

 

نکات مهم این درس

 

انتظار این است که در انتهای این درس شما بتوانید ویژگی های اصلی حل معادلات و نامعادلات به شیوه نموداری را به درستی توضیح داده و برخی کاربردهای آنها را بیان کنید. به ویژه انتظار می رود که بتوانید پرسش های زیر را پاسخ گویید:

 

• روش حل نموداری معادلات و نامعادلات در چه مواقعی به کار می آید؟
• چطور می توانیم یک معادله را به روش نموداری حل کنیم؟
• مزیت نسبی روش جبری حل معادلات به روش نموداری حل آنها، و برعکس، را توضیح دهید.
• نقطه تقاطع نمودار دو معادله چه کمیتی را به دست می دهد؟
• چطور می توانیم یک نامعادله را به روش نموداری حل کنیم؟

 

اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.

 

فراموش نکنیم که بهترین راه برای درک و ” درونی سازی” مفاهیم ریاضی حل مساله است. به همین دلیل سعی کنید دانسته های خود را با حل سوالات زیر محک زده و تقویت کنید.

 

تمرین های درس حل معادلات و نامعادلات به شکل نموداری

 

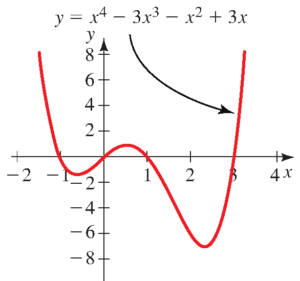
• نمودار معادله $y=x^{4}-3x^{3}-x^{2}+3x$ را در شکل زیر می بینید.
  جواب معادله $ x^{4}-3x^{3}-x^{2}+3x=0$ را به روش نموداری بیابید.
  جواب نامعادله $ x^{4}-3x^{3}-x^{2}+3x \leq 0$ را به روش نموداری بیابید.

 

 

 

• نمودار معادلات $y=5x-x^{2} $ و $y=4 $ را در شکل زیر می بینید.
  جواب معادله $ 5x-x^{2} =4$ را به روش نموداری بیابید.
  جواب نامعادله $ 5x-x^{2} > 4$ را به روش نموداری بیابید.
  1

 

 

• از وبسایت باحساب استفاده کنید و معادلات زیر را به روش جبری و نموداری حل کنید.

 

 

 

• با استفاده از وبسایت باحساب، معادلات زیر را در بازه مورد نظر رسم کرده و جواب معادلات را به دست آورید.

 

 

 

• معادلات زیر را با استفاده از وبسایت باحساب رسم کرده، و جواب معادلات را تا دو رقم اعشار به دست آورید.

 

 

 

• نامعادلات زیر را به روش نموداری با استفاده از وبسایت باحساب حل کنید.

 

 

 

درس بعدی: مدلسازی تغییر در طبیعت

 

بسیاری از پدیده های طبیعی عملا در حال تغییر هستند و یکی از بزرگترین دستاوردهای ریاضیات این است که می تواند تغییر در پدیده های طبیعی را به شیوه روشمند توصیف کند. در درس بعدی درباره مدلسازی این پدیده های در حال تغییر بحث خواهیم کرد و برای اینکار از معادلاتی که تاکنون آموخته ایم استفاده خواهیم کرد.

 

 

 

منابع درس

 

Algebra and Trigonometry, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 4th edition (January 13, 2015)

Precalculus: Mathematics for Calculus, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 7th edition (January 1, 2015)

—–

امیدوارم این درس برای شما مفید بوده باشد. لطفا اگر سوال یا نظری در مورد این درس دارید، با ما درمیان بگذارید.

 درس ها و دوره های دیگری در زمینه ریاضیات، فیزیک و نجوم هم در سایت ما (علمستان) قرار داده شده اند که میتوانید نگاهی به آنها بیندازید.