اندازهگیری، یکاها و ابعاد
در درس قبل مقدمهای بر فیزیک مکانیک گفته شد. در این درس بر اندازهگیری، یکاها و ابعاد تمرکز میکنیم. با تبدیل واحدها کار میکنیم و یاد میگیریم با استفاده از تحلیل ابعادی، از درستی روابط فیزیکی مطمئن شویم.
اندازه گیری و یکاهای اصلی
مرز علم-غیر علم، اندازه گیری دقیق و با معنی است.
بخش هایی از دانش بشری که براساس اندازه گیری های دقیق و سیستماتیک بنا شده اند، در قرون گذشته اهمیت فوق العاده ای پیدا کرده اند. این شاخه های علم تاکنون زندگی روزمره انسان را متحول کرده اند.

دوره مدرن فیزیک، به صورت معنیداری، با دقت اندازه گیری دستگاهها درهمتنیده شده است؛ به این معنا که با افزایش دقت دستگاهها، نظریههای فیزیکی به مراتب بهبود پیدا کردهاند و با بهبود نظریهها، دقت دستگاهها بیشتر شده است.
در علم همیشه درباره کمیتهای “قابل اندازهگیری” صحبت می کنیم. به بیان دقیقتر، کمیتهایی که قابلیت اندازهگیری نداشته باشند، در علوم جایگاهی ندارند.
مثال معاصر: پیشتر کیهانشناسی بیشتر براساس حدسیات فلسفی درباره منشا و شکل جهان بنا شده بود و بنابراین چندان شکل علمی نداشت. ولی در حال حاضر، با اندازهگیریهای دقیق فاصله، فرکانس، زاویه و … این دانش جزء لاینفک فیزیک محسوب شده و بسیاری از حدسیات گذشته رد شده و یا بهبود یافتهاند. این پیشرفتها در کمتر از صد سال اخیر اتفاق افتادهاند.
تمام کمیتهای مطرح در این کتاب، به صورت مستقیم و یا غیرمستقیم، قابل اندازهگیری هستند.
با اندازه گیری برخی از کمیت های پایه (مثل زمان، طول و جرم) و غیر پایه (مثل حجم، چگالی، سرعت، شتاب و …) در آزمایشگاه آشنا خواهید شد.
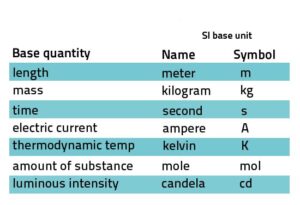
یکاهای اصلی در فیزیک
شکل ها از اینترنت
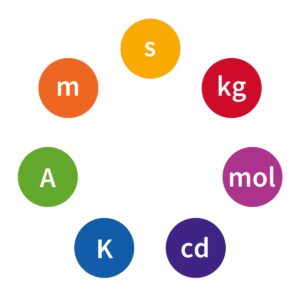
ما برای همه کمیتهای مهم یکا (واحد) تعریف خواهیم کرد؛ ولی تاکنون اثبات شده است که یکای همه کمیتهای فیزیکی را می توان از هفت یکای اصلی طول، جرم، زمان، بار الکتریکی، دما، مقدار ماده و درخشندگی به دست آورد. بنابراین، ما در ابتدا این هفت کمیت اصلی را تعریف کرده و سپس کمیتهای ثانویه را براساس آنها تعریف خواهیم کرد.
مثلا واحد طول، متر $m$ و واحد زمان ثانیه $s$ می باشد؛ بنابراین، واحد سرعت (که آهنگ تغییر در موقعیت است) به صورت $m/s$ به دست می آید. همچنین، شتاب آهنگ تغییر در سرعت می باشد. بنابراین واحد شتاب به صورت $m/s^{2}$ به دست میآید. در انتها، با توجه به اینکه واحد جرم کیلوگرم است، می توان واحد نیرو را با استفاده از قانون دوم نیوتن به صورت زیر به دست آورد:
$F=ma~~~~~~~~\Rightarrow~~~~~~~~N=kg~\frac{m}{s^{2}}$
واحد نیرو را نیوتن $ N $ مینامیم.
پیشتر، یکای کولن $C$ به عنوان واحد بار الکتریکی یکی از یکاهای اصلی به شمار میآمد. ولی اندازهگیری بار الکتریکی مشکل است درحالیکه اندازهگیری برخی کمیتهای وابسته به آن (به ویژه جریان الکتریکی) بسیار راحتتر و دقیقتر است. بنابراین، دانشمندان تصمیم گرفتند که به جای بار الکتریکی از جریان الکتریکی به عنوان یکی از یکاهای اصلی استفاده کنند.
ما در این کتاب از سیستم بینالمللی یکاها SI (Le~ Système~ International~ d’Unités) استفاده خواهیم کرد.
ثانیه: یکای زمان
شکل ها از فیزیک هالیدی، ویرایش پنجم، و ویکیپدیا.
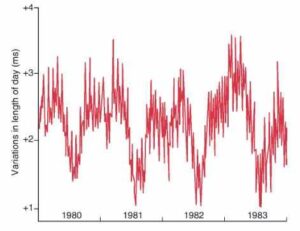
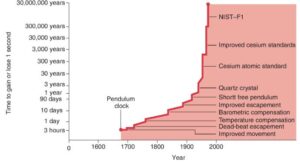
در طول قرون گذشته واحدهای زیادی برای اندازه گیری زمان معرفی شده اند که مشهورترین، و پرکابردترین آنها، سیستم ثانیه-دقیقه-ساعت-روز-سال- قرن… است. این یکاها بر اساس حرکت وضعی و انتقالی زمین ( روز و سال ) معرفی شده اند؛ ولی، اندازه گیری های دقیق نشان داده اند که این مقادیر ثابت نیستند.
هرچند، ما برای دقت هرچه بیشتر، نیاز به ثبات یکاها داریم. به همین دلیل، در قرون گذشته، دستگاه های بسیاری برای اندازه گیری هرچه دقیق تر زمان ابداع شده اند.
دو معیار مهم یک یکای خوب: دقیق بودن و در دسترس بودن.
در حال حاضر از ساعت های اتمی برای اندازه گیری دقیق زمان استفاده می شود.

ثانیه استاندارد:
برابر با 9192631770 زمان تناوب در یک طول موج خاص اتم سزیم 133 می باشد.
متر: یکای طول
فرهنگ های مختلف، تا دو قرن پیش، از یکاهای گوناگونی برای اندازه گیری طول استفاده می کرده اند.
نمونه های ایرانی: ذرع، گز، ارش (یا ارج و یا ذراع)، چارک، گره، بهر و وجب. آیا شما نیز واحد دیگری را برای اندازه گیری طول می شناسید؟
تنوع یکاها امکان تقلب را افزایش می دهد. همچنین، این تنوع مقایسه نتایج علمی را سخت تر می کند. بنابراین، پس از انقلاب فرانسه، در سال 1792 تصمیم بر آن شد که آحاد یکسان و بدون تغییری ایجاد شوند. این تصمیم، در نهایت منجر به تاسیس انجمن بین المللی اوزان و مقادیر شد.
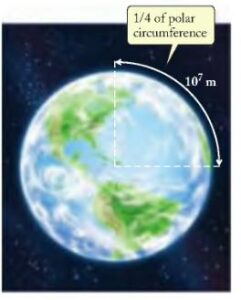
متر در ابتدا به عنوان یک ده میلیونم فاصله استوا تا قطب شمال تعیین شد. ولی این یکا چندان در دسترس همگانی نیست. بنابراین، در ادامه، متر به عنوان فاصله بین دو خراش ریز بر روی یک استوانه از جنس پلاتین-ایریدیم (که در موزه سور پاریس نگهداری می شود) تعریف شد.
مترهای ثانویه دیگری از متر استاندارد تهیه و به نقاط مختلف ارسال شد. ولی، با ساختن هر کپی، دقت مترها کاهش می یابد. چرا؟
در سال 1960، به جهت دستیابی به دقت بیشتر، متر به صورت $1650763.73$ برابر طول موج تابشی نارنجی-قرمز اتم کیپتون-86 تعریف شد.
در نهایت، تا سال 1983، اندازه گیری سرعت نور فوق العاده دقیق تر از اندازه گیری فاصله شده بود. بنابراین، سرعت نور به صورت دقیق
$c=299792458m/s$
تعریف شد. با استفاده از این تعریف، متر استاندارد به صورت فاصله ای تعریف شد که نور در خلاء در زمان $ \frac{1}{299792458} $ میپیماید.
(شکل ها از ویکیپدیا، فیزیک هالیدی، ویرایش دهم و سایت دانشگاه هانوفر آورده شدهاند.)
کیلوگرم: یکای جرم
جرم و وزن نیز در فرهنگ های مختلف با آحاد گوناگونی اندازه گیری می شده اند.
برخی واحدهای جرم و وزن در ایران باستان:
سوت، قیراط، سیر، پانزده، سیه، هفت درم، چارک، صدی، خروار، نخود، مثقال، من (تبریز، اصفهان و …). آیا شما واحد دیگری می شناسید؟
واحد $SI$ جرم استوانه ای از جنس پلاتین-ایریدیم می باشد (شکل زیر) که در موزه سور در نزدیکی پاریس نگهداری می شود.
واحد اتمی جرم ($u$) برابر است با $\frac{1}{12}$ جرم اتم کربن-12:
$1 u = 1.66053886~ \times 10^{-27}~ kg $

تغییرات جدید در سیستم یکاها
اگر مایل هستید با تغییرات اخیر در سیستم بین المللی یکاها آشنا شوید، به سخنرانی آقای دکتر اجتهادی، عضو هیات علمی دانشگاه صنعتی شریف و رییس انجمن فیزیک ایران، در آپارات رجوع کنید.
عنوان سخنرانی:
یک کیلوگرم چقدر است؟ لزوم تغییر کتابهای درسی (لینک مشاهده).
پیشوندها و نمادگذاری علمی
یکاهای SI به صورتی انتخاب شده اند که در محاسبات مربوط به مسائل روزمره، اعداد مورد نظر بسیار بزرگ و یا بسیار کوچک نباشند.
ولی در کاربرد های علمی و فنی، اعداد لزوما از مرتبه یک، ده، صد و غیره نیستند بلکه ممکن است فوقالعاده کوچک و یا فوقالعاده بزرگ باشند. به عنوان مثال، جدول مقادیر زمان، طول و جرم را در ادامه ببینید.
برای کارکردن با این نوع عددها دو راه داریم. نخست، استفاده از پیشوندهاست ( جدول بالا را ملاحظه کنید).
راه دوم استفاده از واحدهای غیر SI ولی هماهنگ با فیزیک مساله است. به عنوان مثال، بخش مربوط به واحدهای نجومی را ببینید (بعدا با یکاهای اتمی آشنا خواهید شد).
واحدهای زاویه
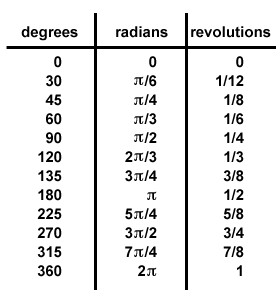
تاکنون یکاهای مختلفی برای اندازه گیری زاویه معرفی شده اند:
- دور.
- درجه: هر دور برابر 360 درجه است.
- گرادیان: هر دور برابر 400 گرادیان است.
- رادیان: هر دور برابر $2\pi$ رادیان است. واحد رادیان اهمیت هندسی و فیزیکی فوق العادهای دارد زیرا روابط فیزیک و ریاضی در این واحد به ساده ترین صورت (بدون ثوابت اضافی) نوشته می شوند.
رابطه اساسی $s=r \theta$ برای طول کمانی از دایره به شعاع $r$ را به خاطر بسپارید. این رابطه فقط و فقط در صورتی درست است که زاویه $\theta$ بر حسب رادیان باشد.
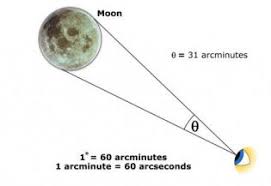
زوایای بسیار کوچک
برای زوایای بسیار کوچک، مخصوصا در نجوم و کیهان شناسی، از دقیقه قوسی و ثانیه قوسی استفاده می شود.
یک درجه برابر با 60 دقیقه قوسی است:
$1^{\circ}=60^{‘}$
یک دقیقه قوسی برابر با 60 ثانیه قوسی است:
$1^{‘}=60^{”}$
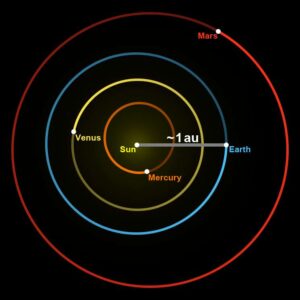
واحدهای نجومی برای منظومه شمسی
واحدهای SI برای اندازه گیری ابعاد منظومه شمسی بسیار کوچکند. بنابراین، در ابعاد منظومه شمسی، از واحد های زیر استفاده می شود:
- سال به عنوان واحد زمان.
- واحد نجومی (AU=Astronomical Unit) به عنوان واحد طول که برابر فاصله میانگین زمین تا خورشید است:
$AU=149597870700 ~m$
- جرم خورشید ($M_{\odot}$) به عنوان واحد جرم:
$M_{\odot}=(1.98847 \pm 0.00007)\times 10^{30}~ kg$
واحدهای نجومی برای کهکشان و ابعاد بزرگتر
در ابعاد کهکشانی، حتی واحدهای نجومی بالا هم چندان مفید نیستند. بنابراین معمولا از واحدهای دیگری استفاده می شود.
واحد زمان: یکی از واحدهای زمانی استفاده شده، طول عمر کیهان است که برابر 13.7 میلیارد سال برآورد شده است. همچنین، از عکس ثابت هابل $\frac{1}{H_{0}}$ به عنوان یک واحد زمانی استفاده می شود (به مساله مربوطه در انتهای درس رجوع کنید).
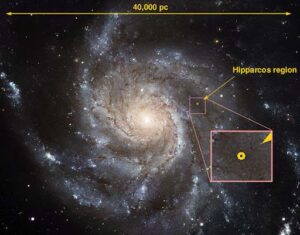
پارسک (pc) به عنوان واحد طول: زاویه یک ثانیه قوسی $1^{”}$ روبه رو به قطاعی به طول یک واحد نجومی $AU$ را در نظر بگیرید. شعاع چنین دایره ای برابر یک پارسک است:
$pc=3.085677581 \times 10^{16} ~m$
واحد جرم: معمولا از ($10^{10}M_{\odot}$) به عنوان واحد جرم استفاده می شود.
لطفا دقت کنید که لازم نیست این یکاها را به خاطر بسپارید. فقط کافی است با این مفهوم آشنا شوید که در هر مساله فیزیکی ممکن است که یکاهای متناسب با آن مساله را تعریف کنیم و باید بدانیم چطور یکاهای مورد استفاده در یک مساله خاص را به یکاهای بین المللی SI تبدیل کنیم.
(شکل ها از ویکیپدیا و http://spiff.rit.edu آورده شدهاند.)
تبدیل واحدها
از قاعده تبدیل زنجیره ای برای تبدیل واحد ها استفاده می کنیم.
مثال: سرعت حرکت زمین به دور خورشید، بنا به تعریف، برابر $2\pi \frac{AU}{year}$ میباشد. این سرعت را برحسب $km/s$ به دست آورید.
پاسخ:
$v=2\pi \frac{AU}{year}=2\pi \frac{149597870700 ~m }{365.25 \times~ 24 \times~ 60 \times~ 60 ~s}$
$v=29785.25~m/s$
بنابراین:
$v \approx 30 km/s$
تمرین: سرعت حرکت خورشید به دور مرکز کهکشان تقریبا برابر $200~km/s$ میباشد. این سرعت را بر حسب $k~pc/year$ به دست آورید.
تحلیل ابعادی
فرمول های فیزیکی باید از لحاظ ابعادی صحیح باشند.
بعد نیرو:
$F=ma~~~~~\Rightarrow~~~~~\left[F \right] = \left[m \right] \left[ a \right]$
$ \left[F \right] = MLT^{-2}$
ثابت های ریاضیاتی ( مثل، 2، 3، $ 5.5 $، $ \pi $، $ e $ و …) بعدی برابر یک دارند:
$\left[ 2 \right] =\left[ 5.5 \right] =\left[ \pi \right] =\left[ e \right] =1$
اکثر ثوابت فیزیکی مثل ثابت گرانش نیوتن $G$، ثابت کولن $K$ و … بعد دارند.
بعد انرژی:
$K=\frac{1}{2}mv^{2}~~~~~\Rightarrow~~~~~ \left[ K \right]=\left[\frac{1}{2}mv^{2} \right] $
$ \left[ K \right]= \left[ \frac{1}{2} \right]\left[ m \right] \left[ v^{2}\right] $
$ \left[ K \right]= 1 \times M~ \left( LT^{-1} \right)^{2} = M L^{2}T^{-2} $
نشان دهید که بعد انرژی پتانسیل
$U=mgh$
هم به همین صورت است.
به لحاظ منطقی انتظار داریم که همه جملاتی که در یک رابطه ریاضیاتی با هم جمع می شوند همجنس باشند ( زیرا مقایسه کردن سیب و پرتقال بی معنی است!).
یعنی در رابطه $a+b+…= c+d+…$ باید جنس کمیت های $a$ ، $b$ ، $c$، و … یکی باشد. برای درک این نکته باید تحلیل ابعادی بدانیم.
بُعد جرم را با $M$، بُعد زمان را با $T$ و بُعد طول را با $L$ نشان می دهیم (در این درس با بعد چهار کمیت اصلی دیگر سروکار نخواهیم داشت). در این صورت می توان به راحتی ابعاد مربوط به هر کمیت دیگر را با استفاده از فرمول مربوطه به دست آورد.
مثلا با توجه به تعریف سرعت متوسط داریم:
$\bar{v}=\frac{\Delta x}{\Delta t}~~~~~\Rightarrow~~~~~\left[ v \right] = \frac{\left[x \right] }{\left[ t \right] }= \frac{L}{T}=LT^{-1}$
نماد $\left[~~ \right] $ نشان دهنده بُعد است.
و یا با توجه به تعریف شتاب متوسط داریم:
$\bar{a}=\frac{\Delta v}{\Delta t}~~~~~\Rightarrow~~~~~\left[ a \right] = \frac{\left[v \right] }{\left[ t \right] }= \frac{LT^{-1}}{T}=LT^{-2}$
دقت کنید که بعد یک کمیت را می توانید از هر فرمول درست دیگر، که شامل آن کمیت است، نیز به دست آورید.
مثال هایی از تحلیل ابعادی
مثال: نیروی کولن بین دو بار الکتریکی $q_{1}$ و $q_{2}$ از رابطه
$F=K\frac{q_{1}q_{2}}{r^{2}}$
به دست می آید. اگر بعد بار الکتریکی را با $C$ نشان دهیم،
$\left[ q \right] =C$
بُعد ثابت کولن $K$ را بیابید.
پاسخ:
$\left[ F\right] =\left[ K\frac{q_{1}q_{2}}{r^{2}} \right] ~~~~ \Rightarrow ~~~~ \left[ K \right] = \frac{\left[ F \right] \left[ r^{2} \right] }{ \left[ q_{1} \right] \left[ q_{2} \right] }$
بنابراین:
$ \left[ K \right] = \frac{MLT^{-2} L^{2} }{ C^{2} }= M L^{3}T^{-2}C^{-2}$
مثال: نیروی گرانش جهانی نیوتن بین دو جرم $m_{1}$ و $m_{2}$ از رابطه
$F=G\frac{m_{1}m_{2}}{r^{2}}$
به دست می آید. بُعد ثابت نیوتن $G$ را بیابید.
پاسخ:
$\left[ F\right] =\left[ G\frac{m_{1}m_{2}}{r^{2}} \right] ~~~~ \Rightarrow ~~~~ \left[ G \right] = \frac{\left[ F \right] \left[ r^{2} \right] }{ \left[ m_{1} \right] \left[ m_{2} \right] }$
بنابراین:
$ \left[ G \right] = \frac{MLT^{-2} L^{2} }{ M^{2} }= L^{3}M^{-1}T^{-2}$
تمرین: اگر شتاب مرکزگرا فقط به سرعت جسم $v$ و فاصله تا مرکز $r$ وابسته باشد، با استفاده از تحلیل ابعادی نشان دهید که این شتاب باید متناسب با
$a \propto v^{2}/r$
باشد. در فصل چهارم رابطه دقیق را به دست خواهیم آورد.
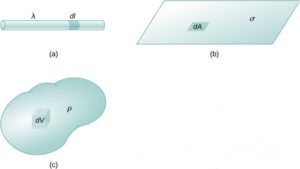
انواع چگالی و چگالی های موضعی
چگالی طولی متوسط:
$ \bar{\lambda} = \frac{M}{L} $
در اینجا $L$ طول کل و $M$ جرم کل جسم است.
چگالی طولی موضعی:
$\lambda = \frac{dM}{dl} $
در اینجا $dl$ المان طول و $dM$ المان جرم است.
در فصل های انتهایی کتاب از این مفاهیم استفاده خواهیم کرد.
چگالی حجمی متوسط:
$ \bar{\rho} = \frac{M}{V} $
در اینجا $V$ حجم کل و $M$ جرم کل جسم است.
چگالی حجمی موضعی:
$ \rho = \frac{dM}{dV} $
در اینجا $dV$ المان حجم و $dM$ المان جرم است.
چگالی سطحی متوسط:
$ \bar{\sigma} = \frac{M}{A} $
در اینجا $A$ مساحت کل و $M$ جرم کل جسم است.
چگالی سطحی موضعی:
$ \sigma = \frac{dM}{dA} $
در اینجا $dA$ المان سطح و $dM$ المان جرم است.
نکات مهم این درس
انتظار این است که در انتهای این درس شما بتوانید نکات اساسی واحدهای اندازه گیری و تحلیل ابعادی را بیان کنید. برای اینکار لازم است بتوانید به سوال های زیر پاسخ دهید:
- چرا اندازه گیری در فیزیک مهم است؟
- واحدهای SI را نام ببرید و اهمیت آنها را توضیح دهید.
- تبدیل یکاها چگونه انجام می شود؟
- نکات اساسی تحلیل ابعادی را بیان کنید.
- انواع چگالی متوسط و موضعی ( و روابط معرف آنها ) را بیان کنید.
اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.
فراموش نکنیم که بهترین راه برای درک و “درونی سازی” مفاهیم ریاضی و فیزیک، حل مساله است. به همین دلیل سعی کنید دانستههای خود را با حل سوالات زیر محک زده و تقویت کنید.
تمرین
تمرینهای بحث یکاها:
۱. جرم سیاره مشتری$ 95.1$ برابر جرم زمین و شعاع آن 120000 کیلومتر است. اگر جرم زمین $6 \times 10^{24} kg$ باشد چگالی مشتری را بیابید.
۲. جرم کهکشان راه شیری، که یک کهکشان دیسکی (قرصی) است، تقریبا $10^{11}$ برابر جرم خورشید، شعاع آن تقریبا 10 کیلوپارسک، و ضخامت آن تقریبا یک کیلوپارسک است. جرم خورشید برابر
$M_{\odot}=2 \times 10^{30} ~~kg$ و هر کیلو پارسک برابر $1 k~pc = 3.1 \times 10^{19} m$ میباشد. چگالی قرص کهکشان را بر حسب kg/m^{3}$ بیابید.
۳. کهکشان کروی مقابل، جرمی تقریبا برابر با $10^{10}$ برابر جرم خورشید دارد و شعاع آن تقریبا 5 کیلوپارسک است. جرم خورشید برابر $M_{\odot}=2 \times 10^{30} ~~kg$ و هر کیلو پارسک برابر $1 k~pc = 3.1 \times 10^{19} m$ می باشد. چگالی این کهکشان را بر حسب $kg/m^{3}$ بیابید.

۴. الف) فرض کنید که $10^{23}$ ستاره هم جرم خورشید در کیهان وجود دارد. جرم کل کیهان را بر حسب کیلوگرم بیابید.
ب)همچنین فرض کنید که کیهان کره ای به شعاع $3000~M~pc$ (مگا پارسک) میباشد. حجم کل کیهان را بر حسب $m^{3}$ بیابید.
پ) چگالی این کره (کیهان) را برحسب $kg/m^{3}$ بیابید.
راهنمایی: جرم خورشید برابر $2 \times 10^{30} kg$ و هر پارسک برابر $pc=3.08\times 10^{16}m$ می باشد.

۵. الف) سال نوری “فاصله” ای است که نور در مدت یک سال می پیماید. هر سال نوری چند متر است؟ راهنمایی: سرعت نور برابر است با $c=3\times 10^{8}~ m/s$.
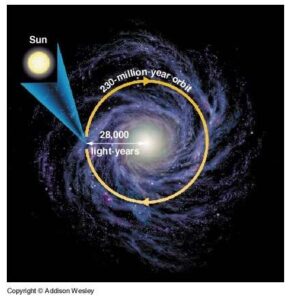
ب) فاصله خورشید تا مرکز کهکشان 28000 سال نوری است. این فاصله چند متر است؟
پ) اگر 230 میلیون سال طول بکشد تا خورشید یکبار به دور کهکشان بچرخد سرعت حرکت خورشید به دور مرکز کهکشان چند متر بر ثانیه است؟ راهنمایی: $v=2\pi r/T$.
ت) شتاب حرکت خورشید به دور مرکز کهکشان را با استفاده از فرمول $a=v^{2}/r$ و بر حسب $m/s^{2}$ به دست آورید.
تمرین های تحلیل ابعادی
۱. در قانون کپلر که به صورت $\frac{R^{3}}{T^{2}}=CM$ نوشته می شود پارامتر $T$ دوره زمانی حرکت سیاره، $R$ فاصله سیاره تا خورشید و $M$ جرم خورشید است. اگر بُعد طول را با $L$، بُعد زمان را با $T$، و بُعد جرم را با $M$ نشان دهیم، بُعد $C$ را بیابید.
۲. بعد چگالی های حجمی، سطحی و طولی را بیابید.
۳. بنا به قانون هابل که به صورت $v=Hr$ نوشته می شود، سرعت کهکشان های بسیار دوردست $( v )$ با فاصله ی آنها از ما $( r )$ متناسب است. اگر بُعد طول را با $L$، بُعد زمان را با $T$، و بُعد جرم را با $M$، نشان دهیم، الف) ابعاد سرعت $( v )$ و فاصله $( r )$ را بنویسید. ب) بعد ثابت $H$ را بیابید.
۴. مقدار ثابت هابل تقریبا برابر $H_{0} \simeq 70~\frac{km/s}{M~pc}$ برآورد شده است. در اینجا داریم $M~pc=10^{6}~pc$. الف) مقدار این ثابت را برحسب $1/s$ بیابید. ب) مقدار $\frac{1}{H_{0}}$ تخمینی از عمر کیهان است. این مقدار را بر حسب سال بیابید.
۵. اگر یک ستاره به جرم $M$ به شعاع $r=2GM/c^{2}$ برسد رمبش کرده و به یک سیاهچاله تبدیل می شود! در اینجا $c$ سرعت نور است. اگر بُعد طول را با $L$، بُعد زمان را با $T$، و بُعد جرم را با $M$ نشان دهیم، الف) بُعد $c$ را بیابید. ب) بُعد $G$ را بیابید.
۶. نیروی پسار $D$ (نوعی نیرویی اصطکاکی) در سیالی که چگالی $\rho$ دارد، به جسمی که با سرعت $v$ و با مساحت مقطع $A$ در سیال حرکت می کند برابر $D=1/2C\rho Av^{2}$ می باشد. در این رابطه $C$ یک ضریب تناسب است. اگر بُعد طول را با $L$، بُعد زمان را با $T$، و بُعد جرم را با $M$، نشان دهیم، بُعد $C$ را بیابید. راهنمایی: در ابتدا بُعد نیرو $D$، چگالی $\rho$، سرعت $v$ و مساحت $A$ را بیابید.
۷. انرژی پتانسیل $U$ یک مولکول دو اتمی که در فاصله $r$ از هم قرار دارند به صورت $U=\frac{A}{r^{12}}-\frac{B}{r^{6}}$ می باشد. اگر بُعد طول را با $L$، بُعد زمان را با $T$، و بُعد جرم را با $M$، نشان دهیم، بُعد ثابت های $A$ و $B$ را بیابید. راهنمایی: در ابتدا بُعد انرژی $U$ را بیابید.
شناخت دقیق تر پارسک
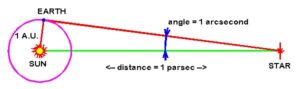
الف) یک ثانیه قوسی را برحسب رادیان بیابید.
ب) در شکل بالا، زاویه یک ثانیه قوسی $1^{”}$ روبه رو به قطاعی به طول یک واحد نجومی $AU$ را در نظر بگیرید. شعاع چنین دایره ای برابر یک پارسک است. با استفاده از رابطه $s=r \theta$ نشان دهید که
$pc=3.085677581 \times 10^{16} ~m$
پ) یک پارسک چند سال نوری است؟
مبحث بعدی: حرکت در راستای خط راست
در فصل بعدی، حرکت در راستای خط راست ( حرکت یک بعدی ) را بررسی خواهیم کرد. شناخت این حرکت پایه اساسی شناخت حرکت های کلی است زیرا، همانطور که بعدا نشان خواهیم داد، حرکت های چند بعدی ترکیبی از چند حرکت یک بعدی هستند.

مراجع
Halliday, David, Robert Resnick, and Jearl Walker; Fundamentals of physics, 10th ed. John Wiley $\&$ Sons, 2014
Halliday, D., R. Resnick, and K. S. Krane. “Physics, 5th ed.” (2002).
Ohanian, Hans C., and John T. Markert. Physics for engineers and scientists, 3rd ed. 2007.
Young, Hugh D., Roger A. Freedman, and Albert Lewis Ford. Sears and Zemansky’s University Physics, 13th edn. Pearson Education, 2006.
\par