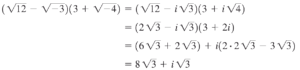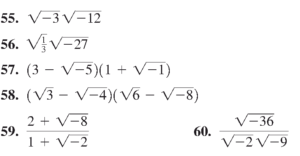۹- ویژگی های اعداد مختلط

در درس قبل با اعداد مختلط آشنا شدیم. در اینجا به جزئیات بیشتری از ویژگی های اعداد مختلط میپردازیم.

ا

آنچه گذشت: مقدمه ای بر اعداد مختلط

 

• تعریف عدد مختلط: یک عدد مختلط عددی به شکل $a+bi $ می باشد که در آن $a$ و $b $ اعداد حقیقی هستند و $i^{2}=-1$. عدد $a$ را قسمت حقیقی و عدد $b $ را قسمت موهومی عدد مختلط $a+bi $ می نامند.
  ا

• نکته: دو عدد مختلط با هم برابرند اگر و فقط اگر قسمت حقیقی آن دو برابر باشد و قسمت موهومی آنها نیز برابر باشد:

$ a+bi=x+yi~~~~~\Leftrightarrow~~~~~a=x~~~and~~~b=y~~~~$

• عدد مختلطی مانند $z=a+bi$ را در نظر بگیرید. در این صورت، مزدوج مختلط این عدد مختلط به صورت $\bar{z}=a-bi$ تعریف می شود.

 

• جمع اعداد مختلط:

$ (a+bi)+(c+di)=(a+c)+(b+d)i$

• تفریق اعداد مختلط:

$(a+bi)-(c+di)=(a-c)+(b-d)i $

 

• ضرب اعداد مختلط:

$  (a+bi) \times (c+di)=(ac-bd)+(ad+bc)i $

 

• تقسیم اعداد مختلط:

$ \frac{a+bi}{c+di}=\left( \frac{a+bi}{c+di} \right) \left( \frac{c-di}{c-di} \right)=\frac{(ac+bd)+(bc-ad)i}{c^{2}+d^{2}}$

 

 

ویژگی های اعداد مختلط: ریشه دوم اعداد منفی

 

همانطور که هر عدد حقیقی مثبت مانند $r$ دو ریشه دوم به صورت $\sqrt{r}$ و $-\sqrt{r}$ دارد، هر عدد حقیقی منفی مانند $-r$ نیز دو ریشه دوم دارد. در واقع، اگر $-r$ یک عدد منفی باشد دو ریشه دوم آن اعداد $\pm i \sqrt{r}$ می باشند زیرا

 

$ (i \sqrt{r})^{2}=i^{2}r=-r,~~~~~~~~~~~~~~~~~~~~(-i \sqrt{r})^{2}=(-1)^{2}i^{2}r=-r$

 

اگر $-r$ یک عدد حقیقی منفی باشد آنگاه ریشه دوم اصلی $-r$ برابر

$ \sqrt{-r}=i\sqrt{r}$

می باشد. دو ریشه $-r$ برابر $~i\sqrt{r}~$ و $~-i\sqrt{r}~$ هستند.

 

توجه کنید که معمولا می نویسیم $i\sqrt{b}$ و نه $\sqrt{b}i$؛ زیرا می خواهیم نمادگذاری ما باعث سردرگمی بین $\sqrt{b}i$ و $\sqrt{bi}$ نشود.

 

به محاسبات زیر دقت کنید:

 

$ \sqrt{-1}=i\sqrt{1}=i$

$\sqrt{-16}=i\sqrt{16}=4i$

$ \sqrt{-3}=i\sqrt{3}=i\sqrt{3}$

 

اشتباه نکنیم!

 

باید در هنگام محاسبات مربوط به ریشه دوم اعداد منفی بسیار مراقب باشیم. مخصوصا دقت کنید که رابطه $\sqrt{a}\sqrt{b}=\sqrt{ab}$ برای اعداد مثبت درست است ولی وقتی هر دو عدد منفی هستند، درست نیست! مثلا دقت کنید:

 

$  \sqrt{-2}\sqrt{-3}=i\sqrt{2}i\sqrt{3}=i^{2}\sqrt{6}=-\sqrt{6}$

ولی از طرفی داریم

$  \sqrt{(-2)(-3)} = \sqrt{6}$

بنابراین

$   \sqrt{-2}\sqrt{-3} \neq \sqrt{(-2)(-3)}$.

 

 

نکته مهم: برای جلوگیری از چنین اشتباهاتی، وقتی رادیکال اعداد منفی را در هم ضرب می کنید اول آنها را به شکل $i\sqrt{r}$ بنویسید ($r>0$) و سپس محاسبات را ادامه دهید.

 

مثال:  نتیجه $(\sqrt{12}-\sqrt{-3})(3-\sqrt{-4})$ را به شکل $a+bi$ بنویسید.

پاسخ:

 

 

 

ویژگی های اعداد مختلط: جواب های مختلط معادله درجه دوم

 

تاکنون دیده ایم که جواب معادله درجه دوم $ax^{2}+bx+c=0$، به شرط $a \neq 0$، به صورت زیر است:

 

$  x_{1,2}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

 

همچنین، فهمیدیم که اگر $b^{2}-4ac <0$ آنگاه معادله مورد نظر جواب حقیقی ندارد. هرچند، در چنین حالتی معادله مورد نظر در مجموعه اعداد مختلط جواب دارد؛ زیرا اعداد منفی در مجموعه اعداد مختلط ریشه مربعی دارند.

 

مثال: جواب معادله $x^{2}+9=0$ را بیابید.

پاسخ: معادله بالا یعنی $x^{2}=-9$؛ در نتیجه داریم:

$ x=\pm \sqrt{-9}=\pm i \sqrt{9}=\pm 3i$

 

مثال: جواب معادله $x^{2}+4x+5=0$ را بیابید.

پاسخ: با استفاده از جواب عمومی معادله درجه دوم داریم:

 

$ x_{1,2}=\frac{-4 \pm \sqrt{4^{2}-4(1)(5)}}{2}=\frac{-4 \pm \sqrt{-4}}{2}= \frac{-4 \pm 2i}{2}=-2\pm i$

 

بنابراین معادله $x^{2}+4x+5=0$ دو جواب مختلط به صورت $-2+i$ و $-2-i$ دارد.

 

از مثال قبل، و در واقع از فرم کلی جواب معادله درجه دوم، می توان فهمید که اگر معادله درجه دومی دارای جواب های مختلط باشد، آنگاه این جواب ها مزدوج مختلط هم هستند.

 

جواب های معادله درجه دوم، مزدوج مختلط هم هستند.

 

مثال: نشان دهید که جواب های معادله درجه دوم $4x^{2}-24x+37=0$ مزدوج مختلط هم هستند.

پاسخ: با استفاده از جواب عمومی معادله درجه دوم داریم:

 

$ x_{1,2}=\frac{24 \pm \sqrt{24^{2}-4(4)(37)}}{2(4)}=\frac{24 \pm \sqrt{-16}}{8}= \frac{24 \pm 4i}{8}=3 \pm \frac{1}{2} i$

 

بنابراین معادله $4x^{2}-24x+37=0$ دو جواب مختلط به صورت $3 + \frac{1}{2} i$ و $3 – \frac{1}{2} i$ دارد که مزدوج مختلط هم هستند.

 

 

نکات مهم درس ویژگی های اعداد مختلط

 

انتظار این است که در انتهای این درس شما بتوانید ویژگی های اصلی اعداد مختلط را به درستی توضیح داده و برخی کاربردهای آنها را بیان کنید. به ویژه انتظار می رود که بتوانید پرسش های زیر را پاسخ گویید:

 

• ریشه دوم یک عدد منفی مانند $-r$ در مجموعه اعداد مختلط را بنویسید.
• توضیح دهید که چرا $\sqrt{-2}\sqrt{-3} \neq \sqrt{(-2)(-3)}~~~~$. برای جلوگیری از چنین اشتباهاتی باید چکار کنیم؟
• توضیح دهید که چرا اگر معادله درجه دومی ریشه مختلط داشته باشد آنگاه آن دو ریشه مزدوج مختلط هم هستند.

اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.

 

فراموش نکنیم که بهترین راه برای درک و ” درونی سازی” مفاهیم ریاضی حل مساله است. به همین دلیل سعی کنید دانسته های خود را با حل سوالات زیر محک زده و تقویت کنید.

 

 

تمرین های درس ویژگی های اعداد مختلط

 

• هرکدام از رادیکال های زیر را محاسبه کرده و نتیجه را به شکل $a+bi$ بنویسید.

 

 

 

 

• جواب معادلات زیر را یافته و نتیجه را به شکل $a+bi$ بنویسید.

 

 

• اگر داشته باشیم $z=3-4i$ و $w=5+2i$ نتیجه عبارت های زیر را بیابید.یادآوری از جلسه قبل: $\bar{q}$ به معنی مزدوج مختلط عدد $q$ می باشد.

 

 

 

• اگر داشته باشیم $z=a+bi$ و $w=c+di$ تساوی های زیر را اثبات کنید.
  
  یادآوری از جلسه قبل: $\bar{q}$ به معنی مزدوج مختلط عدد $q$ می باشد.

 

1. $ \bar{w}+\bar{z}=\overline{w+z}$
2. $\bar{w} \bar{z}=\overline{w z}$
3. $ (\bar{z})^{2}=\bar{z^{2}}$
4. $  \bar{ \bar{z}}=z$
5. عبارت $ \bar{z}+z$ حقیقی است.
6. عبارت $ z- \bar{z}$ موهومی است.
7. عبارت $ \bar{z} z$ حقیقی است.
8. عبارت $ \bar{z}= z$ فقط و فقط وقتی درست است که $ z$ حقیقی باشد.

 

منابع برای مطالعات بیشتر

 

مبحث متغیرهای مختلط و کاربردهای آنها در رشته های گوناگون دانشگاهی، و به شیوه های متفاوت، در نظر گرفته می شود. هرچند، برای بررسی ساختاری این موضوع بهتر است به کتاب های ریاضیاتی مراجعه کنید. اگر قصد دارید این مبحث را به صورت نسبتا پیشرفته، ولی خلاصه، پیگیری کنید توصیه می کنم به دوفصل توابع مختلط کتاب “روش های ریاضی در فیزیک”، نوشته آرفکن و وبر، مراجعه کنید.

 

 

 

 

درس بعدی: حل انواع دیگر معادلات

 

در جلسه بعد حل برخی چندجمله ای های ساده و معادلات شامل رادیکال ها را بررسی خواهیم کرد.

 

 

منابع درس

 

Algebra and Trigonometry, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 4th edition (January 13, 2015)

Precalculus: Mathematics for Calculus, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 7th edition (January 1, 2015)

 

—–

امیدوارم این درس برای شما مفید بوده باشد. لطفا اگر سوال یا نظری در مورد این درس دارید، با ما درمیان بگذارید.

 درس ها و دوره های دیگری در زمینه ریاضیات، فیزیک و نجوم هم در سایت ما (علمستان) قرار داده شده اند که میتوانید نگاهی به آنها بیندازید.