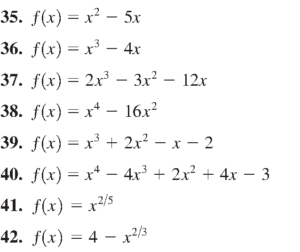۶. توابع افزایشی و کاهشی؛ نقاط بیشینه و کمینه تابع

در درس قبل با استخراج اطلاعات از نمودار توابع آشنا شدیم. در این درس در مورد توابع افزایشی و کاهشی؛ نقاط بیشینه و کمینه تابع صحبت میکنیم.

م

آنچه گذشت: استخراج اطلاعات از نمودار توابع

 

• نمودار کامل یک تابع همه اطلاعات تابع را در خود دارد، به این دلیل که نمودار تابع به ما می گوید چه مقادیر ورودی به چه مقادیر خروجی مربوط است. یعنی همه نقاط $(x,~f(x)~)$ را به ما می دهد.

 

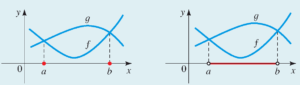
• پیدا کردن دامنه و برد یک تابع از روی نمودار: دامنه و برد یک تابع مانند $y=f(x)$ را می توان از روی نمودار تابع، مانند شکل زیر، تشخیص داد. دامنه مجموعه همه مقادیر $x$ است که برای آنها تابع $f(x)$ تعریف شده است. برد نیز مجموعه همه $y$ های متناظر است.

 

• جواب های معادله $f(x)=g(x)$ مقادیری از $ x $ هستند که نمودارهای توابع $f$ و $g$ همدیگر را قطع می کنند.

 

• جواب های نامعادله $f(x)<g(x)$ مقادیری از $ x $ هستند که نمودار تابع $g$ بالاتر از نمودار تابع $f$ قرار می گیرد.

 

        1

 

 

توابع افزایشی و کاهشی

 

افزایش و کاهش در نمودار توابع

 

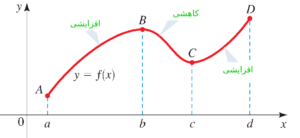
یکی از رفتارهای بسیار مهم نمودار توابع، روند بالارفتن و پایین آمدن نمودار آنهاست. مثلا، نمودار شکل زیر، وقتی از مبدا به سمت مثبت محور افقی می رویم، بالا رفته (از نقطه $A$ به $B$) و سپس پایین می آید (از نقطه $B$ به $C $) و در انتها نیز دوباره بالا می رود (از نقطه $C$ به $D $).

 

تابع $f$ را افزایشی (صعودی) می گوییم وقتی که نمودار آن از سمت چپ به راست بالا می رود.
1

تابع $ f$ را کاهشی (نزولی) می گوییم وقتی که نمودار آن از سمت چپ به راست پایین می آید.

 

در نمودار زیر، تابع $f$ در بازه $\left(a,~b \right)$ افزایشی، در بازه $\left(b,~c \right)$ کاهشی (Decreasing) و در بازه $\left(a,~b \right)$ دوباره افزایشی (Increasing) است.

 

 

 

تعریف توابع افزایشی و کاهشی

 

• تابع $f$ در یک بازه افزایشی است اگر هرگاه $x_{1}<x_{2}$ آنگاه $f(x_{1})<f(x_{2})$.
  1
• تابع $f$ در یک بازه کاهشی است اگر هرگاه $x_{1}<x_{2}$ آنگاه $f(x_{1})>f(x_{2})$.

 

برای درک این رفتار به صورت شهودی، شکل زیر را ببینید.

 

دقت کنید که تعریف تابع افزایشی و کاهشی مربوط به رفتار تابع در یک «بازه» است. به صورت مشخص، صحبت کردن از کاهشی و افزایشی بودن توابع در یک نقطه بی معنی است.

 

به مثال های زیر دقت کنید.

 

 

وزن افراد به عنوان تابعی از زمان

 

وزن افراد مدام در حال تغییر است. معمولا وزن افراد در ابتدا اضافه می شود، مدتی ثابت باقی می ماند، سپس دوباره اضافه و بعدا کم می شود. اکثر افراد نیز در دوره های آخر عمر خود وزن تقریبا ثابتی دارند.

 

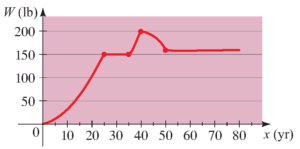
در شکل زیر وزن یک نفر (Weight) به عنوان تابعی از سن او رسم شده است. تعیین کنید که وزن این فرد در چه بازه هایی افزایشی و کاهشی است؟

 

پاسخ: وزن این فرد در بازه های$(0,~25)$ و $(35,~40)$ افزایشی است. همچنین، وزن او در بازه های $(40,~50)$ کاهشی است.

 

نکته: معمولا افزایشی و کاهشی بودن رفتار تابع را با بازه های باز نشان می دهیم. این قراردادی است که ما در این مجموعه درس حفظ خواهیم کرد. هرچند، نشان دادن افزایشی و کاهشی بودن رفتار تابع با بازه های بسته نیز قابل قبول است.

 

 

پیدا کردن بازه های کاهشی و افزایشی در رفتار توابع

 

مثال 1: تابع $f(x)=12x^{2}+4x^{3}-3x^{4}$ را رسم کنید. سپس دامنه و برد آن را از روی شکل تعیین کنید. آنگاه بازه هایی را که تابع بر روی آنها افزایشی و کاهشی است معلوم کنید.

 

 

نمودار تابع را در شکل بالا می بینید. دامنه این تابع، بنا به شکل، همه مقادیر حقیقی است؛ یعنی $\mathbb{R}$. برد تابع نیز بازه $\left( -\infty,~32 \right]$ را تشکیل می دهد (باید در نرم افزار مورد نظر بر روی بالاترین نقطه کلیک کنید تا داده های آن معلوم شود). همچنین، از نمودار مقابل معلوم است که $f(x)$ در بازه $(-\infty,-1)$ و $(0,~2)$ افزایشی ( صعودی ) است و در بازه های $(-1,~0)$ و $(2,~\infty)$ کاهشی ( نزولی ) است.

 

 

مثال 2: تابع $f(x)= x^{\frac{2}{3}} $ را رسم کنید. سپس دامنه و برد آن را از روی شکل تعیین کنید. آنگاه بازه هایی را که تابع بر روی آنها افزایشی و کاهشی است معلوم کنید.

 

 

نمودار تابع را در شکل بالا می بینید. دامنه این تابع، بنا به شکل، همه مقادیر حقیقی است؛ یعنی $\mathbb{R}$. برد تابع نیز بازه $\left[0,~\infty \right)$ را تشکیل می دهد. همچنین، از نمودار مقابل معلوم است که $f(x)$ در بازه $(-\infty,~0)$ کاهشی (نزولی) است و در بازه های $(0,~\infty)$ افزایشی (صعودی) است.

 

 

بیشینه و کمینه موضعی توابع

 

بیشترین و کمترین مقادیر توابع

 

پیدا کردن کوچکترین و بزرگترین مقادیر توابع کاربردهای بسیاری دارد. در واقع بسیاری از مسائل فیزیکی بر مبنای پیدا کردن کوچکترین و بزرگترین مقدار حل می شوند. ولی اجازه دهید مثالی ساده تر را در نظر بگیریم: فرض کنید که تابعی نشان دهنده سود یک شرکت است. در این صورت ما همیشه می خواهیم که این سود بیشترین باشد. از طرفی، اگر تابع هزینه های شرکت را داشته باشیم، آنگاه بهترین حالت این است که هزینه ها کمترین باشد. مقادیر بیشینه (بیشترین) و کمینه (کمترین) یک تابع را می توان به راحتی از روی نمودار آن تابع یافت. هرچند، بهتر است در ابتدا بیشینه و کمینه موضعی توابع (Local Maximum and Minimum) را تعریف کنیم.

 

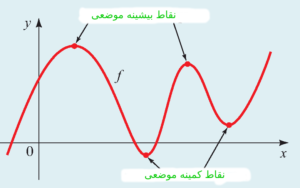
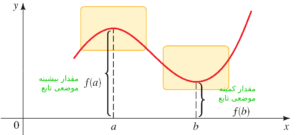
• مقدار $ f(a) $ را مقدار بیشینه موضعی تابع $  f $ می نامند اگر برای هر نقطه $ x $ نزدیک به نقطه $ a $ داشته باشیم $  f(a) \geq f(x)$. یعنی مقدار تابع در نقطه $ a$ از مقدار تابع در هر نقطه همسایگی اش بیشتر باشد. شکل زیر را ببینید.

 

• مقدار $ f(a) $ را مقدار کمینه موضعی تابع $ f$ می نامند اگر برای هر نقطه $ x $ نزدیک به نقطه $ a$ داشته باشیم $ f(a) \leq f(x)$. یعنی مقدار تابع در نقطه $ a $ از مقدار تابع در هر نقطه همسایگی اش کمتر باشد. شکل زیر را ببینید.

 

فعلا، نقاط بیشینه و کمینه، و مقدار بیشینه و کمینه تابع در این نقاط را، با استفاده از نمودارها بدست می آوریم. هرچند، بعدا یاد می گیریم که پیدا کردن نقاط بیشینه و کمینه موضعی یکی از اصلی ترین کاربردهای مفهوم مشتق است.

 

 

 

برای پیدا کردن مقادیر بیشینه و کمینه موضعی توابع، نمودار این توابع را رسم می کنیم.

 

• اگر یک مستطیل در نزدیکی یک نقطه مانند $\left(a,~f(a) \right)$ داشته باشیم به صورتی که مقدار تابع در این نقطه از مقدار تابع در همه نقاط دیگر مستطیل بیشتر باشد، یعنی $ f(a) \geq f(x) $، آنگاه می گوییم مقدار $ f(a) $ یک بیشینه موضعی تابع $ f $ است. شکل زیر را ببینید.

 

• اگر یک مستطیل در نزدیکی یک نقطه مانند $\left(b,~f(b) \right)$ داشته باشیم به صورتی که مقدار تابع در این نقطه از مقدار تابع در همه نقاط دیگر مستطیل کمتر باشد، یعنی $ f(b) \leq f(x) $، آنگاه می گوییم مقدار $ f(b) $ یک کمینه موضعی تابع $ f $ است. شکل زیر را ببینید.

 

 

 

مثال

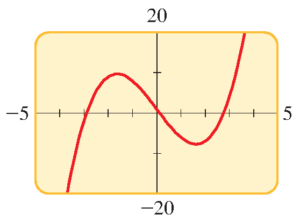
مقادیر کمینه موضعی ($local ~minimum$) و بیشینه موضعی ($local ~maximum$) تابع $f(x)=x^{3}-8x+1$ را با استفاده از رسم نمودار بیابید.

1

پاسخ: در ابتدا نمودار را رسم می کنیم ( شکل بالا ). بنا به این نمودار، بیشینه موضعی تابع در بازه $(-2,-1)$ و کمینه موضعی آن در بازه $(1,2)$ رخ می دهد.

 

هرچند، برای یافتن مکان و مقدار بیشینه و کمینه موضعی باید نمودار را در بازه های کوچکتر رسم کرده و سعی کنیم روی این نقاط تمرکز کنیم. پس از کمی سعی و خطا به دو نمودار زیر برای بیشینه و کمینه می رسیم.

 

                               ۱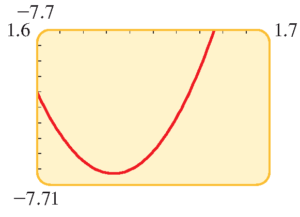     

 

با توجه به این نمودارها، بیشینه موضعی تابع تقریبا در نقطه $(-1.63,9.71)$ و کمینه موضعی آن در نقطه $(1.63,-7.71)$ رخ می دهند. پس، مقدار تابع در بیشینه موضعی برابر $ 9.71 $ و مقدار آن در کمینه موضعی برابر $ -7.71$ می باشد.

 

 

مدلی برای پیش بینی ترافیک

 

یک مهندس ترافیک رابطه ای را برای پیش بینی تعداد ماشین های موجود در یک بزرگراه، که با سرعت خاصی حرکت می کنند، بدست آورده است. او فرض می کند که هر ماشین 17 فوت طول دارد، با سرعت $x$ حرکت می کند و نسبت به ماشین جلویی در فاصله ایمن قرار دارد. به این ترتیب او درمی یابد که تعداد ماشینی که در دقیقه از محل خاصی عبور می کنند با رابطه

 

$N=\frac{88x}{17+17(\frac{x}{20})^{2}}$

 

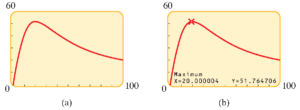
داده می شود. الف) نمودار این تابع را رسم کنید. ب) در چه بازه هایی این تابع صعودی و در چه بازه هایی نزولی است؟ پ) مقدار بیشینه تابع را بیابید. این مقدار در چه سرعتی اتفاق می افتد؟

 

پاسخ: نمودار را در شکل زیر می بینید. این نمودار در بازه $(0,~20)$ افزایشی ( صعودی ) است و در بازه $(20,~\infty)$ کاهشی ( نزولی ) است. مقدار بیشینه تابع $ N $ نیز در $ N \approx 50$ رخ می دهد (مقدار دقیق $ N = 51.76$ می باشد).

 

 

 

نکات مهم این درس

 

انتظار این است که در انتهای این درس شما بتوانید ویژگی های اصلی توابع افزایشی و کاهشی و همچنین نقاط بیشینه و کمینه توابع را به درستی توضیح داده و برخی کاربردهای آنها را بیان کنید. به ویژه انتظار می رود که بتوانید پرسش های زیر را پاسخ گویید:

 

• به صورت شهودی، چه تابعی را افزایشی (صعودی) می گوییم؟ تعریف دقیق ریاضی تابع افزایشی را بنویسید.
• به صورت شهودی، چه تابعی را کاهشی (نزولی) می گوییم؟ تعریف دقیق ریاضی تابع کاهشی را بنویسید.
• توضیح دهید که رفتار افزایشی و یا کاهشی توابع مربوط به یک بازه است یا یک نقطه؟
• چطور می توان بازه های افزایشی و یا کاهشی یک تابع را از روی نمودار تشخیص داد؟
• چه مقداری از تابع را بیشینه موضعی آن تابع می گویند؟
• بیشینه موضعی یک تابع را چطور می توان از روی نمودار پیدا کرد؟
• چه مقداری از تابع را کمینه موضعی آن تابع می گویند؟
• کمینه موضعی یک تابع را چطور می توان از روی نمودار پیدا کرد؟

 

اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.

 

فراموش نکنیم که بهترین راه برای درک و ” درونی سازی” مفاهیم ریاضی حل مساله است. به همین دلیل سعی کنید دانسته های خود را با حل سوالات زیر محک زده و تقویت کنید.

 

 

تمرین

 

• با استفاده از نمودار توابع زیر،

1.  دامنه و برد توابع را بیابید.
2.  بازه هایی را که در آن توابع مورد نظر کاهشی و یا افزایشی اند معلوم کنید.

 

 

• برای توابع $f$ زیر،

1.  نمودار توابع را با استفاده از نرم افزار رسم کنید.
2.  دامنه و برد توابع را بیابید.
3. بازه هایی را که نمودار در آنها کاهشی و یا افزایشی است به صورت تقریبی بیان کنید.

 

 

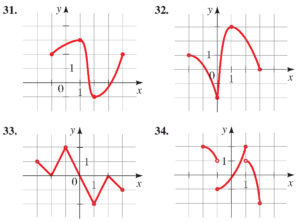
• با استفاده از نمودار توابع زیر،

1.  نقاط بیشینه و کمینه توابع (مقادیر $x$ و $y$ این نقاط را) تعیین کنید.
2.  بازه هایی را که در آن توابع مورد نظر کاهشی و یا افزایشی اند معلوم کنید.

 

 

• برای توابع $f$ زیر،

1. نمودار توابع را با استفاده از نرم افزار رسم کنید.
2.  دامنه و برد توابع را بیابید.
3. بازه هایی را که نمودار در آنها کاهشی و یا افزایشی است به صورت تقریبی بیان کنید.
4. نقاط بیشینه و کمینه توابع را بیابید.

 

 

درس بعدی: آهنگ متوسط تغییر در یک تابع

 

از توابع معمولا برای توصیف کمیت های در حال تغییر استفاده می کنیم. در درس بعد یاد خواهیم گرفت که چطور آهنگ تغییر در خروجی تابع، وقتی که ورودی تابع تغییر می کند، را بیابیم.

 

         ۱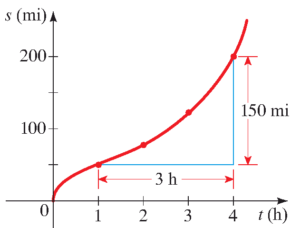

 

 

 

 

 

منابع درس

 

Algebra and Trigonometry, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 4th edition (January 13, 2015)

Precalculus: Mathematics for Calculus, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 7th edition (January 1, 2015)

 

—–

امیدوارم این درس برای شما مفید بوده باشد. لطفا اگر سوال یا نظری در مورد این درس دارید، با ما درمیان بگذارید.

 درس ها و دوره های دیگری در زمینه ریاضیات، فیزیک و نجوم هم در سایت ما (علمستان) قرار داده شده اند که میتوانید نگاهی به آنها بیندازید.