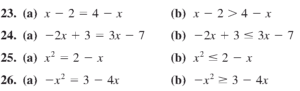۵. استخراج اطلاعات از نمودار توابع

در درس قبل با نحوه تشخیص توابع آشنا شدیم. در این درس با استخراج اطلاعات از نمودار توابع بیشتر آشنا میشویم.

آنچه گذشت: تشخیص تابع

 

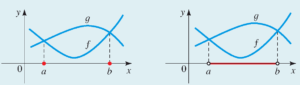
• آزمون خط عمود برای تشخیص توابع از روی منحنی: منحنی رسم شده در دستگاه مختصات نشان دهنده منحنی یک تابع است اگر و فقط اگر هر خط عمودی منحنی را حداکثر در یک نقطه قطع کند. شکل زیر را ببینید.

 

• تشخیص توابع با توجه به رابطه آنها: معادله مورد نظر را برای پیدا کردن $y$ حل می کنیم. اگر به ازای هر $x$ در دامنه عبارت جبری فقط یک $y$ پیدا شد، آنگاه می گوییم که عبارت جبری مورد نظر یک تابع است. ولی اگر به ازای هر $x$ در دامنه عبارت جبری بیش از یک $y$ پیدا شد، آنگاه می گوییم که عبارت جبری مورد نظر تابع نیست.
  1
  تابع است:

$y-x^{2}=2~~~~~~\Rightarrow~~~~~~y=x^{2}+2$

1    تابع نیست:

$x^{2}+y^{2}=4~~~~~~\Rightarrow~~~~~~y^{2}=4-x^{2}~~~~~~\Rightarrow~~~~~~y =\pm \sqrt{4-x^{2}}$

 

 

 

مقدار یک تابع؛ دامنه و برد

 

مقدار یک تابع

 

بسیاری از ویژگی های یک تابع را می توان از روی نمودار آن، بسیار راحت تر از رابطه آن، بدست آورد.

 

در واقع، نمودار کامل یک تابع همه اطلاعات تابع را در خود دارد، به این دلیل که نمودار تابع به ما می گوید چه مقادیر ورودی به چه مقادیر خروجی مربوط است. یعنی همه نقاط $(x,~f(x)~)$ را به ما می دهد.

 

برای تحلیل نمودار یک تابع باید در ذهن داشته باشیم که ارتفاع منحنی در هر نقطه $x$ از محور افقی، نشان دهنده مقدار تابع در آن نقطه، یعنی $f(x) $، است. بنابراین می توان مقادیر یک تابع را از نمودار آن خواند.

 

مثلا نمودار زیر مقدار دما ( بر حسب فارنهایت ) در یک ایستگاه هواشناسی را از نیمروز تا ساعت 6 بدست می دهد. با استفاده از این نمودار می توان اطلاعات بسیاری بدست آورد.

 

نمودار تغییرات دما

 

 

نمودار بالا مقدار دما ( بر حسب فارنهایت ) در یک ایستگاه هواشناسی را از نیمروز تا ساعت 6 بعدازظهر بدست می دهد.

 

الف) مقادیر $T(1)$، $T(3)$ و $T(5)$ را بیابید.

پاسخ: $T(1)$ مقدار دما در ساعت یک بعدازظهر است، و …

$T(1)=25,~~~~~~~~~~~~T(3)=30,~~~~~~~~~~~~T(5)=20 $

1
ب) دما در ساعت دو بیشتر است یا ساعت چهار؟

پاسخ: ارتفاع نمودار در $x=2$ بیشتر از ارتفاع نمودار در $x=4$ می باشد؛ بنابراین $T(2)>T(4)~~$.

 

پ) در چه زمان هایی دما 25 درجه فارنهایت است؟

پاسخ: باید زمان هایی را بیابیم که در آنها مقدار دما برابر 25 است. یعنی زمان هایی که نمودار خط افقی $T=25$ را قطع می کند. بنا به نمودار، این اتفاق در زمان های $x=1$ و $x=4$ می افتد.

 

ت) در چه زمان هایی دما بیشتر از 25 درجه فارنهایت است؟

پاسخ: باید زمان هایی را بیابیم که در آنها مقدار دما بیشتر از 25 است. یعنی زمان هایی که نمودار بالای خط افقی $T=25$ قرار می گیرد. بنا به نمودار، این اتفاق در زمان های بین $1 \leq x \leq 4$ می افتد.

 

ث) تغییر کل در دما از ساعت 1 تا 3 بعدازظهر چقدر است؟

پاسخ:

$T(3)-T(1)=30-25=5 $

بنابراین دما از ساعت 1 تا 3 بعدازظهر به اندازه 5 درجه فارنهایت افزایش یافته است.

 

 

دامنه و برد یک نمودار

 

نمودار یک تابع به ما کمک می کند تا دامنه و برد آن تابع را بیابیم.

 

 

به این نکته توجه کنید:

 

پیدا کردن دامنه و برد یک تابع از روی نمودار: دامنه و برد یک تابع مانند $y=f(x)$ را می توان از روی نمودار تابع، مانند شکل مقابل، تشخیص داد. دامنه مجموعه همه مقادیر $x$ است که برای آنها تابع $f(x)$ تعریف شده است. برد نیز مجموعه همه $y$ های متناظر است.

 

نمودار تابع $f(x)=\sqrt{4-x^{2}}$، که یک نیمدایره است، را در شکل زیر می بینید. با توجه به این شکل، دامنه و برد تابع را بیابید.

 

 

پاسخ: با استفاده از شکل می بینیم که بازه تغییرات $x$، و یا همان دامنه، به صورت $\left[-2,~2\right]$ می باشد در حالی که بازه تغییرات $y$، و یا برد، به صورت $\left[0,~2\right]$ است.

 

 

مقایسه مقادیر تابع؛ حل نموداری معادلات و نامعادلات

 

مقایسه مقادیر توابع

1

ما می توانیم مقادیر دو تابع $f$ و $g$ را از روی نمودار آنها با هم مقایسه کنیم.

 

در نقاطی که دو تابع همدیگر را قطع می کنند، مقدار دو تابع با هم برابر می شود. بنابراین، جواب های معادله $f(x)=g(x)$ نقاطی هستند که نمودار دو تابع همدیگر را قطع می کنند.

 

نقاطی که نمودار تابع $g(x)$ بالاتر از نمودار تابع $f(x)$ قرار گرفته است نقاطی هستند که مقدار تابع $g(x)$ بیشتر از مقدار تابع $f(x)$ می باشد. بنابراین، جواب های نامعادله $f(x)<g(x)$ نقاطی از محور $ x $ هستند که نمودار تابع $g(x)$ بالاتر از نمودار تابع $f(x)$ قرار گرفته است.

 

جواب های معادله $f(x)=g(x)$ مقادیری از $ x $ هستند که نمودارهای توابع $f$ و $g$ همدیگر را قطع می کنند.

 

جواب های نامعادله $ f(x)<g(x)$ مقادیری از $x $ هستند که نمودار تابع $ g$ بالاتر از نمودار تابع $f$ قرار می گیرد.

 

 

 

مثال اول

 

معادله و نامعادلات زیر را به صورت نموداری حل کنید.

 

 

پاسخ:

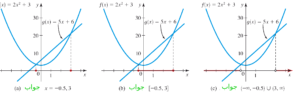
در ابتدا باید با استفاده از نرم افزاری مانند متمتیکا، نمودار دو تابع $f(x)=2x^{2}+3$ و $g(x)=5x+6$ را به صورت همزمان رسم کنیم. نتیجه را در شکل های زیر می بینید.

 

پاسخ ($a$): با توجه به توضیحات بالا، پاسخ این معادله مقادیری از $ x $ است که نمودارهای توابع $f$ و $g$ همدیگر را قطع می کنند. بنابراین، با توجه به شکل، نقاط $x=-0.5$ و $x=3$ جواب های این معادله اند.

 

پاسخ $b$): با توجه به اسلایدهای قبل، پاسخ این نامعادله مقادیری از $ x $ است که نمودار تابع $f$ پایینتر و یا همسطح با نمودار تابع $g$ قرار می گیرد.. بنابراین، با توجه به شکل، بازه $\left[-0.5,~3 \right]$ جواب این نامعادله است.

 

پاسخ ($c$): با توجه به اسلایدهای قبل، پاسخ این نامعادله مقادیری از $ x $ است که نمودار تابع $f$ بالاتر از نمودار تابع $g$ قرار می گیرد.. بنابراین، با توجه به شکل، بازه $\left(-\infty,~-0.5 \right) \cup \left(3,~\infty \right)$ جواب این نامعادله است.

 

 

 

یک تمرین و یک نکته

 

تمرین: معادله و نامعادلات مثال قبل را به شیوه جبری حل کنید (با استفاده از روش های گفته شده در دوره ریاضیات پایه: معادلات و نمودارها).

 

همانطور که در دوره ریاضیات پایه: معادلات و نمودارها نیز بحث شد، برای حل معادلات و نامعادلات به صورت نموداری می توان همه جملات را به یک سمت رابطه منتقل کرد و سپس نمودار عبارت جبری حاصله را رسم کرد.

1

به مثال بعدی دقت کنید.

 

مثال دوم

 

معادله و نامعادله زیر را به صورت نموداری حل کنید.

 

 

پیداکردن جواب معادله: در ابتدا همه جملات را به یک سمت منتقل می کنیم تا معادله جدیدی بدست آید.

حال، بر این اساس تابع جدیدی تعریف کرده

و نمودار آن را رسم می کنیم. شکل زیر را ببینید ( سمت چپ ). نقاط تقاطع نمودار با محور افقی جواب معادله مورد نظر ما هستند.

 

 

 

پیداکردن جواب نامعادله: باز هم به همین روش عمل می کنیم. فقط در این حالت باید نامعادله $f(x) \geq 0$ را حل کنیم؛ یعنی مجموعه نقاطی از نمودار تابع که بالای محور افقی قرار گرفته اند. جواب را در شکل بالا، سمت راست، ببینید.

 

 

نکات مهم این درس

 

انتظار این است که در انتهای این درس شما بتوانید ویژگی های اصلی استخراج اطلاعات از نمودار توابع را به درستی توضیح داده و برخی کاربردهای آنها را بیان کنید. به ویژه انتظار می رود که بتوانید پرسش های زیر را پاسخ گویید:

 

• آیا نمودار یک تابع همه اطلاعات آن تابع را در خود دارد؟ چرا؟
• در نمودار تابع، ارتفاع منحنی در هر نقطه نسبت به محور افقی نشان دهنده چه کمیتی است؟
• دامنه یک تابع را چطور از روی نمودار آن تابع تشخیص می دهیم؟
• برد یک تابع را چطور از روی نمودار آن تابع تشخیص می دهیم؟
• اگر نمودار دو تابع $f(x)$ و $g(x)$ را به صورت همزمان رسم کنیم، جواب معادله $f(x)=g(x)$ در چه نقاطی رخ می دهد؟
• اگر نمودار دو تابع $f(x)$ و $g(x)$ را به صورت همزمان رسم کنیم، جواب نامعادله $f(x)>g(x)$ در چه نقاطی رخ می دهد؟
• آیا می توان به جای حل معادله $f(x)=g(x)$ معادله $f(x)-g(x)=0$ را حل کرد؟ جواب های این معادله در چه نقاطی از نمودار تابع $f(x)-g(x) $ رخ می دهند؟

 

اگر درباره هرکدام از مفاهیم یاد شده بالا مشکلی احساس می کنید، لطفا درس را یک بار دیگر مرور کنید.

 

فراموش نکنیم که بهترین راه برای درک و ” درونی سازی” مفاهیم ریاضی حل مساله است. به همین دلیل سعی کنید دانسته های خود را با حل سوالات زیر محک زده و تقویت کنید.

 

 

تمرین

 

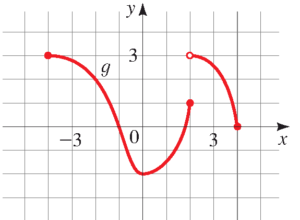
• نمودار تابع $g$ در زیر داده شده است.
  ۱
  الف) مقادیر $g(-4)$، $g(-2)$، $g(0)$، $g(2)$ و $g(4)$ را بیابید.
  ب) دامنه و برد تابع $g$ را بیابید.
  پ) معادله $g(x)=3$ را حل کنید.
  ت) نامعادله $g(x)\leq 0$ را حل کنید.
  ث) تغییر کل در تابع بین نقاط $x=-1$ تا $x=2$ را بیابید.

 

 

1

• نمودار تابع $h$ در زیر داده شده است.
  ۱
  الف) مقادیر $h(-2)$، $h(0)$، $h(2)$ و $h(3)$ را بیابید.
  ب) دامنه و برد تابع $h$ را بیابید.
  پ) معادله $h(x)=3$ را حل کنید.
  ت) نامعادله $h(x)\leq 3$ را حل کنید.
  ث) تغییر کل در تابع بین نقاط $x=-3$ تا $x=3$ را بیابید.

 

 

 

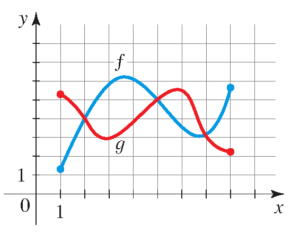
• نمودار توابع $f$ و $g$ در زیر داده شده است.
  ۱
  الف) مقدار $f(6)$ بزرگتر است یا $g(6)$؟
  ب) مقدار $f(3)$ بزرگتر است یا $g(3)$ ؟
  پ) معادله $f(x)=g(x)$ را حل کنید.
  ت) نامعادله $f(x) \leq g(x)$ را حل کنید.
  ث)نامعادله $f(x) > g(x)$ را حل کنید.

 

 

• نمودار توابع $f$ و $g$ در زیر داده شده است.
  ۱
  الف) مقدار $f(0)$ بزرگتر است یا $g(0)$ ؟
  ب) مقدار $f(-3)$ بزرگتر است یا $g(-3)$ ؟
  پ) معادله $f(x)=g(x)$ را حل کنید.
  ت) نامعادله $f(x) \leq g(x)$ را حل کنید.
  ث)نامعادله $f(x) > g(x)$ را حل کنید.

 

1

• برای توابع $f$ زیر،
  ۱
  الف) نمودار توابع را با استفاده از نقطه یابی رسم کنید.
  ب) دامنه و برد تابع را با استفاده از نمودار تابع بیابید.

 

 

• برای توابع $f$ زیر،
  ۱
  الف) نمودار توابع را با استفاده از یک نرم افزار و یا وبسایت محاسب رسم کنید.
  ب) دامنه و برد تابع را با استفاده از نمودار تابع بیابید.

 

 

• معادلات و نامعادلات زیر را به شیوه رسم نمودار حل کنید (بهتر است از یک نرم افزار و یا وبسایت محاسب استفاده کنید).

 

 

• معادلات و نامعادلات زیر را به شیوه رسم نمودار حل کنید (بهتر است از یک نرم افزار و یا وبسایت محاسب استفاده کنید).

 

 

درس بعدی: توابع افزایشی و کاهشی؛ نقاط بیشینه و کمینه تابع

 

در جلسه بعد خواهیم آموخت که چطور می توان توابع افزایشی و کاهشی را تشخیص داد. همچنین با نقاط بیشینه و کمینه توابع آشنا خواهیم شد.

 

 

 

 

منابع درس

 

Algebra and Trigonometry, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 4th edition (January 13, 2015)

Precalculus: Mathematics for Calculus, by James Stewart, Lothar Redlin, and Saleem Watson, Cengage Learning; 7th edition (January 1, 2015)

—–

امیدوارم این درس برای شما مفید بوده باشد. لطفا اگر سوال یا نظری در مورد این درس دارید، با ما درمیان بگذارید.

 درس ها و دوره های دیگری در زمینه ریاضیات، فیزیک و نجوم هم در سایت ما (علمستان) قرار داده شده اند که میتوانید نگاهی به آنها بیندازید.